
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() 是
是![]() 边上一点,
边上一点,![]() ,
,![]() 平分
平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() .
.

(1)若![]() ,求
,求![]() 和
和![]() 的度数;
的度数;
(2)若![]() ,求证
,求证![]() .
.
【答案】(1)70°;30°;(2)见解析
【解析】
(1)根据等边对等角求出∠CAB和∠CBA的度数,再根据等边对等角求出∠BEC和∠BCE的度数,从而可得出∠ACE的度数,最后根据外角的性质可求出∠BEC的度数;再证明△BCF≌△BEF,从而得出∠BEF的度数,最后得出∠FEC的度数.
(2)先根据(1)中全等得出EF=CF,再由等角对等边判定△AEF为等腰三角形,得出AE=EF,从而得出结果.
证明:(1)∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() 平分
平分![]() ,∴∠CBF=∠EBF,
,∴∠CBF=∠EBF,
在△BCF和△BEF中,

∴△BCF≌△BEF(SAS).
∴∠BEF=∠BCF=100°,.
∴∠FEC=∠BEF-∠BEC=30°.
(2)由(1)可知![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.


科目:初中数学 来源: 题型:
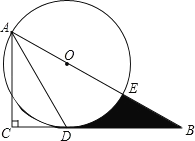
【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地有两条公路,一条是全长600km的普通公路,另一条是全长480km的高速公路,某客车在高速公路上行驶的平均速度比在普通公路上快45![]() /
/![]() ,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的角分线.
(1)以AB上的一点O为圆心,AD为弦在图中作出⊙O.(不写作法,保留作图痕迹);
(2)试判断直线BC与⊙O的位置关系,并证明你的结论.
(3)若∠B=30°,计算S△DAC:S△ABC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于检修部分生产设备,生产能力下降,某工厂现在比原计划平均每天少生产30台机器,现在生产600台机器所需时间与原计划生产900台机器所需时间相同.
问现在平均每天生产多少台机器.
(1)设现在平均每天生产![]() 台机器,则用含
台机器,则用含![]() 的式子表示;
的式子表示;
原计划平均每天生产______台机器,现在生产600台机器所需时间为______天,原计划生产900台机器所需时间为______天;
(2)列出方程,完成本题解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B(3,3)在双曲线![]() (x>0)上,点D在双曲线
(x>0)上,点D在双曲线![]() (x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(1)求k的值;
(3)求点A的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,BC=10,tan∠ABC=![]() ,点O是AB边上的动点,以O为圆心,OB为半径的⊙O与边BC的另一交点为D,过点D作AB的垂线,交于点E,连结BE、AE.
,点O是AB边上的动点,以O为圆心,OB为半径的⊙O与边BC的另一交点为D,过点D作AB的垂线,交于点E,连结BE、AE.
(1)当AE∥BC(如图(1))时,求⊙O的半径;
(2)设BO=x,AE=y,求y关于x的函数关系式;
(3)若以A为圆心的⊙A与⊙O有公共点D、E,当恰好也过点C时,求DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com