
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 经过点M(1,3)和N(3,5)
经过点M(1,3)和N(3,5)
(1)试判断该抛物线与x轴交点的情况;
(2)平移这条抛物线,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A、O、B为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.

【答案】(1)抛物线与x轴没有交点;(2)先向左平移3个单位,再向下平移3个单位或将原抛物线先向左平移2个单位,再向下平移5个单位.
【解析】
试题分析:(1)把M、N两点的坐标代入抛物线解析式可求得a、b的值,可求得抛物线解析式,再根据一元二次方程根的判别式,可判断抛物线与x轴的交点情况;
(2)利用A点坐标和等腰三角形的性质可求得B点坐标,设出平移后的抛物线的解析式,把A、B的坐标代入可求得平移后的抛物线的解析式,比较平移前后抛物线的顶点的变化即可得到平移的过程.
试题解析:
(1)由抛物线过M、N两点,把M、N坐标代入抛物线解析式可得:![]() ,解得:
,解得:![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ,令y=0可得
,令y=0可得![]() ,该方程的判别式为△=9﹣4×1×5=9﹣20=﹣11<0,∴抛物线与x轴没有交点;
,该方程的判别式为△=9﹣4×1×5=9﹣20=﹣11<0,∴抛物线与x轴没有交点;
(2)∵△AOB是等腰直角三角形,A(﹣2,0),点B在y轴上,∴B点坐标为(0,2)或(0,﹣2),可设平移后的抛物线解析式为![]() :
:
①当抛物线过点A(﹣2,0),B(0,2)时,代入可得:![]() ,解得:
,解得:![]() ,∴平移后的抛物线为
,∴平移后的抛物线为![]() ,∴该抛物线的顶点坐标为(
,∴该抛物线的顶点坐标为(![]() ,
,![]() ),而原抛物线顶点坐标为(
),而原抛物线顶点坐标为(![]() ,
,![]() ),∴将原抛物线先向左平移3个单位,再向下平移3个单位即可获得符合条件的抛物线;
),∴将原抛物线先向左平移3个单位,再向下平移3个单位即可获得符合条件的抛物线;
②当抛物线过A(﹣2,0),B(0,﹣2)时,代入可得:![]() ,解得:
,解得:![]() ,∴平移后的抛物线为
,∴平移后的抛物线为![]() ,∴该抛物线的顶点坐标为(
,∴该抛物线的顶点坐标为(![]() ,
,![]() ),而原抛物线顶点坐标为(
),而原抛物线顶点坐标为(![]() ,
,![]() ),∴将原抛物线先向左平移2个单位,再向下平移5个单位即可获得符合条件的抛物线.
),∴将原抛物线先向左平移2个单位,再向下平移5个单位即可获得符合条件的抛物线.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
乙班 | 100 | 95 | 110 | 91 | 104 | 500 |
经统计发现两班总数相等.此时有学生建议,可以通过考察数据中的其他信息作为参考.
请你回答下列问题:
(1)计算两班的优秀率.
(2)计算两班比赛数据的方差.
(3)根据以上信息,你认为应该把冠军奖杯发给哪一个班级?简述你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列四个选项中,不适合普查的是
A. 了解全班同学每周体育锻炼的时间
B. 学校招聘新教师,对应聘教师面试
C. 鞋厂检查生产鞋底能承受的弯折次数
D. 安庆市某中学调查九年级全体540名学生数学成绩
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④![]()
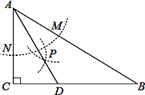
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从四边形的一个顶点出发,可得一条对角线;从五边形的一个顶点出发可得二条对角线;从六边形的一个顶点出发可得三条对角线;…按此规律,从n(n≥4,且n是整数)边形的一个顶点出发可得对角线条.
查看答案和解析>>
科目:初中数学 来源: 题型:
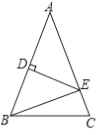
【题目】如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB=________cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com