Question

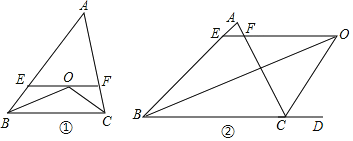
【题目】（1）如图①，△ABC中，∠ABC、∠ACB的平分线交于O点，过O点作EF∥BC交AB、AC于点E、F，试猜想EF、BE、CF之间有怎样的关系，并说明理由；

（2）如图，若将图①中∠ACB的平分线改为外角∠ACD的平分线，其它条件不变，请直接写出EF、BE、CF之间的关系　 　．

Answer 1

【答案】（1）EF＝BE+CF，理由见解析；（2）EF＝BE﹣CF，理由见解析

【解析】

（1）等腰三角形有△BEO和△CFO，根据角平分线性质和平行线性质推出∠EBO＝∠EOB，∠FOC＝∠FCO，根据等角对等边推出即可；根据BE＝OE，CF＝OF即可得出EF与BE、CF之间的关系；

（2）等腰三角形有△BEO和△CFO，根据角平分线性质和平行线性质推出∠EBO＝∠EOB，∠FOC＝∠FCO，根据等角对等边推出即可；根据BE＝OE，CF＝OF即可得出EF与BE、CF之间的关系．

（1）EF＝BE+CF，

理由：∵BO平分∠ABC，CO平分∠ACB，

∴∠EBO＝∠OBC，∠FCO＝∠OCB，

∵EF∥BC，

∴∠EOB＝∠OBC，∠FOC＝∠OCB，

∴∠EBO＝∠EOB，∠FOC＝∠FCO，

∴BE＝OE，CF＝OF，

∴EF＝OE+OF＝BE+CF；

（2）不成立，

理由：∵BO平分∠ABC，CO平分∠ACG，

∴∠EBO＝∠OBC，∠FCO＝∠OCG，

∵EF∥BC，

∴∠EOB＝∠OBC，∠FOC＝∠OCG，

∴∠EBO＝∠EOB，∠FOC＝∠FCO，

∴BE＝OE，CF＝OF，

∴EF＝OE﹣OF＝BE﹣CF．

故答案为EF＝BE﹣CF．