
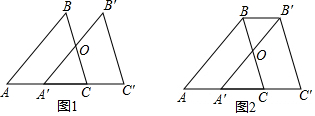
分析 (1)根据AB∥A'B',得到∠A=∠B′A′C′,根据相似三角形的性质得到∠ACB=∠C′由平行线的判定即可得到结论;
(2)由平移的性质得到BC=B′C′,BB′=CC′=3cm,即可得到结论.
解答 解:(1)BC与B'C'平行,
理由:∵AB∥A'B',
∴∠A=∠B′A′C′,
∵∠B=∠B',
∴△ABC∽△A′B′C′,
∴∠ACB=∠C′
∴BC∥B'C';
(2)∵将△ABC沿边AC向右平移3 cm得到△A'B'C',
∴BC=B′C′,BB′=CC′=3cm,
∴四边形ABB'C'的周长=AB+AC+B′C′+B′B+CC′=AB+AC+BC+6,
∵△ABC的周长为16 cm,
∴四边形ABB'C'的周长=22cm.
点评 本题考查了平移的性质,平行线的判定和性质,熟练掌握平移的性质是解题的关键.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | -6 | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 13个 | B. | 12个 | C. | 16个 | D. | 15个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
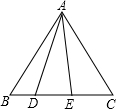 在等边三角形ABC中,点D在BC上,且BD:DC=1:4,连接DA,作∠DAE,满足∠DAE=30°,则tan∠BAE的值是$\frac{\sqrt{3}}{2}$.
在等边三角形ABC中,点D在BC上,且BD:DC=1:4,连接DA,作∠DAE,满足∠DAE=30°,则tan∠BAE的值是$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$(环) | 8.4 | 8.6 | 8.6 | 7.6 |
| S2 | 0.74 | 0.56 | 0.94 | 1.92 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com