
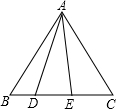
 在等边三角形ABC中,点D在BC上,且BD:DC=1:4,连接DA,作∠DAE,满足∠DAE=30°,则tan∠BAE的值是$\frac{\sqrt{3}}{2}$.
在等边三角形ABC中,点D在BC上,且BD:DC=1:4,连接DA,作∠DAE,满足∠DAE=30°,则tan∠BAE的值是$\frac{\sqrt{3}}{2}$. 分析 在△ABC外作∠BAF=30°,∵∠DAE=30°,得到∠BAF=∠DAE,过D作DF⊥AF于F,DG⊥AC于G,过B作BH⊥AC于H,设△ABC的边长为a,求得BH=$\frac{\sqrt{3}}{2}$a,推出四边形AFDG是矩形,根据矩形的性质得到AF=DG,DF=AG,根据平行线分线段成比例定理得到$\frac{HG}{CH}=\frac{BD}{BC}$=$\frac{1}{5}$,得到AG=$\frac{a}{2}$+$\frac{a}{10}$=$\frac{3}{5}$a=DF,根据三角函数的定义即刻得到结论.
解答  解:在△ABC外作∠BAF=30°,
解:在△ABC外作∠BAF=30°,
∵∠DAE=30°,
∴∠BAF=∠DAE,过D作DF⊥AF于F,DG⊥AC于G,过B作BH⊥AC于H,
设△ABC的边长为a,
则BH=$\frac{\sqrt{3}}{2}$a,
∵BD:DC=1:4,
∴$\frac{DG}{BH}$=$\frac{CD}{BC}$=$\frac{4}{5}$,
∴DG=$\frac{4}{5}$BH=$\frac{2\sqrt{3}}{5}$a,
∵∠F=∠FAG=∠AGD=90°,
∴四边形AFDG是矩形,
∴AF=DG,DF=AG,
∴AF=$\frac{2\sqrt{3}}{5}$a,
∵DG∥BH,
∴$\frac{HG}{CH}=\frac{BD}{BC}$=$\frac{1}{5}$,
∴HG=$\frac{1}{5}$CH=$\frac{a}{10}$,
∴AG=$\frac{a}{2}$+$\frac{a}{10}$=$\frac{3}{5}$a=DF,
∴tan∠BAE=tan∠DAF=$\frac{\frac{3}{5}a}{\frac{2\sqrt{3}}{5}a}$=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查了平行线分线段成比例定理,矩形的判定和性质,解直角三角形,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:填空题
 如图,在直角坐标系中,直线l与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则C3的坐标是(-16$\sqrt{3}$,64);Cn的坐标是(-22(n-1)$\sqrt{3}$,22n)(n为正整数).
如图,在直角坐标系中,直线l与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则C3的坐标是(-16$\sqrt{3}$,64);Cn的坐标是(-22(n-1)$\sqrt{3}$,22n)(n为正整数).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
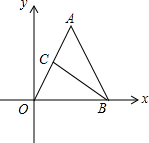 如图,在直角坐标系中有一个等腰△AOB,点O为坐标原点,AO=AB,OB=4,tan∠AOB=2,点C是线段OA的中点.
如图,在直角坐标系中有一个等腰△AOB,点O为坐标原点,AO=AB,OB=4,tan∠AOB=2,点C是线段OA的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
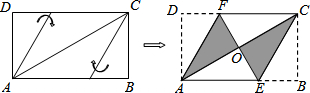 将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为 ( )
将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为 ( )| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
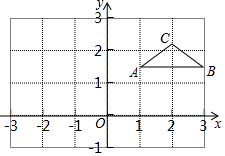 如图,△ABC在平面直角坐标系内,它的三个顶点的坐标分别为A(1,$\sqrt{2}$),B(3,$\sqrt{2}$),C(2,$\sqrt{5}$),求△ABC的面积.
如图,△ABC在平面直角坐标系内,它的三个顶点的坐标分别为A(1,$\sqrt{2}$),B(3,$\sqrt{2}$),C(2,$\sqrt{5}$),求△ABC的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com