
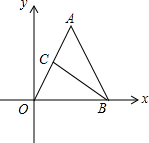
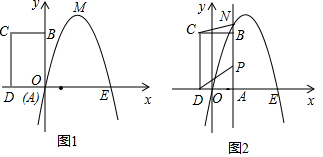
 如图,在直角坐标系中有一个等腰△AOB,点O为坐标原点,AO=AB,OB=4,tan∠AOB=2,点C是线段OA的中点.
如图,在直角坐标系中有一个等腰△AOB,点O为坐标原点,AO=AB,OB=4,tan∠AOB=2,点C是线段OA的中点.分析 (1)过点A作AH⊥OB于点H,首先求出点A坐标,再求出线段OA的中点C的坐标即可.
(2)由于∠APO=∠CBO,所以由(1)可知:tan∠APO=tan∠CBO=$\frac{2}{3}$,从而可知PD=6,设P(x,0),可知|x-2|=6,解出x的值后,利用待定系数法即可求出抛物线的解析式;
(3)若△MAD∽△AOB,则∠MAN=∠AOB,由于(2)问中由两个抛物线解析式,所以分两种情况讨论,由于切点N的不确定性,所以点N的位置由两种,一种是点N在点A的上方,另一种是点N在点A的下方.
解答 解:(1)如图1中,过点A作AH⊥OB于点H.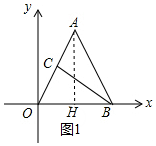
∵AO=AB,AH⊥OB,
∴OH=$\frac{1}{2}$OB=2,
∵tan∠AOB=2,
∴AH=4,
∴点A的坐标为(2,4).
∵C是OA的中点,
∴点C的坐标为(1,2).
(2)由(1)可知:A的坐标为(2,4),
∵∠APO=∠CBO,
∴tan∠APO=tan∠CBO=$\frac{2}{3}$,
∴$\frac{AH}{PH}$=$\frac{2}{3}$,
∴PH=6,
设P的坐标为(x,0),
∵H(2,0),
∴PH=|x-2|
∴|x-2|=6,
∴x=8或x=-4,
∴P(8,0)或(-4,0);
当P的坐标为(8,0)时,
把A(2,4)和(8,0)代入y=ax2+bx,
∴$\left\{\begin{array}{l}{4=4a+b}\\{0=64a+8b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=\frac{8}{3}}\end{array}\right.$,
∴抛物线的解析式为:y=-$\frac{1}{3}$x2+$\frac{8}{3}$x,
当P的坐标为(-4,0)时,
把A(2,4)和P(-4,0)代入y=ax2+bx,
∴$\left\{\begin{array}{l}{4=4a+2b}\\{0=16a-4b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{b=\frac{4}{3}}\end{array}\right.$,
∴抛物线的解析式为:y=$\frac{1}{3}$x2+$\frac{4}{3}$x,
综上所述,抛物线的解析式为:y=-$\frac{1}{3}$x2+$\frac{8}{3}$x或y=$\frac{1}{3}$x2+$\frac{4}{3}$x;
(3)当抛物线的解析式为y=-$\frac{1}{3}$x2+$\frac{8}{3}$x时,如图2,
当△MAD∽△AOB时,
∵△AOB是等腰三角形,
∴∠MAD=∠AOB,
①若点N在A的上方时,
此时∠MAN=∠AOB,
∴AM∥x轴,
∴M的纵坐标为4,
∴把y=4代入y=-$\frac{1}{3}$x2+$\frac{8}{3}$x,
解得:x=2(舍去)或x=6,
∴M的坐标为(6,4),
②如图3中,当点N在点A的下方时,此时∠MAN=∠AOB,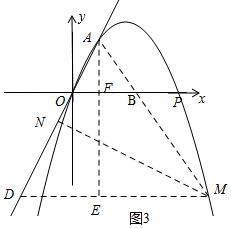
∴DM∥x轴,
过点A作AE⊥DM于点E,交于x轴于点F
∴DE=2-a,
∵tan∠MDA=tan∠AOB=2,
∴AE=2DE=4-2a
∴由勾股定理可知:AD=$\sqrt{5}$(2-a)
∴$\frac{OA}{DM}$=$\frac{OB}{AD}$,
∴DM=$\frac{5(2-a)}{4}$,设M的横坐标为x,
∴x-a=$\frac{5(2-a)}{4}$.
∴x=$\frac{10-a}{4}$,
∴M( $\frac{10-a}{4}$,2a)
把M( $\frac{10-a}{4}$,2a)代入y=-$\frac{1}{3}$x2+$\frac{8}{3}$x,
∴2a=-$\frac{1}{3}$( $\frac{10-a}{4}$)2+$\frac{8}{3}$×( $\frac{10-a}{4}$)
解得:a=2或a=-110
∴当a=2时,M(2,4)舍去
当a=-110时,M(30,-220)
当抛物线的解析式为y=$\frac{1}{3}$x2+$\frac{4}{3}$x时,如图4,
若点N在点A的上方时,
此时∠MAN=∠AOB,
延长MA交x轴于点F,
∵∠MAN=∠OAF,
∴∠AOB=∠OAF,
∴FA=FO,
过点F作FG⊥OA于点G,
∵A(2,4),
∴由勾股定理可求得:AO=2 $\sqrt{5}$,
∴OG=$\frac{1}{2}$AO=$\sqrt{5}$,
∵tan∠AOB=$\frac{GF}{OG}$,
∴GF=2 $\sqrt{5}$,
∴由勾股定理可求得:OF=5,
∴F的坐标为(5,0),
设直线MA的解析式为:y=mx+n,
把A(2,4)和F(5,0)代入y=mx+n,
∴$\left\{\begin{array}{l}{4=2k+b}\\{0=5k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=\frac{20}{3}}\end{array}\right.$,
∴直线MA的解析式为:y=-$\frac{4}{3}$x+$\frac{20}{3}$,
联立 $\left\{\begin{array}{l}{y=\frac{1}{3}{x}^{2}+\frac{4}{3}x}\\{y=-\frac{4}{3}x+\frac{20}{3}}\end{array}\right.$,
∴解得:x=2(舍去)或x=-10,
把x=-10代入y=-$\frac{4}{3}$x+$\frac{20}{3}$,
∴y=20,
∴M(-10,20),
若点N在点A的下方时,
此时∠MAN=∠AOB,
∴AM∥x轴,
∴M的纵坐标为4,
把y=4代入y=$\frac{1}{3}$x2+$\frac{4}{3}$x,
∴x=-6或x=2(舍去),
∴M(-6,4),
综上所述,存在这样的点M(6,4)或(-10,20)或(-6,4),使得△MAD∽△AOB.
点评 本题考查二次函数的综合问题,涉及勾股定理,待定系数法求解析式,解方程,垂直平分线的性质等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | -6 | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 13个 | B. | 12个 | C. | 16个 | D. | 15个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
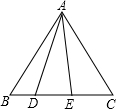 在等边三角形ABC中,点D在BC上,且BD:DC=1:4,连接DA,作∠DAE,满足∠DAE=30°,则tan∠BAE的值是$\frac{\sqrt{3}}{2}$.
在等边三角形ABC中,点D在BC上,且BD:DC=1:4,连接DA,作∠DAE,满足∠DAE=30°,则tan∠BAE的值是$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
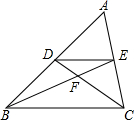 如图,在任意△ABC中,DE∥BC,连接BE与CD相交于点F,则下列结论一定正确的有几个( )
如图,在任意△ABC中,DE∥BC,连接BE与CD相交于点F,则下列结论一定正确的有几个( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com