
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() 且与直线
且与直线![]() :
:![]() 平行,直线
平行,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点B、C.
轴分别交于点B、C.
(1)求直线l1的表达式及其与![]() 轴的交点D的坐标;
轴的交点D的坐标;
(2)判断四边形ABCD是什么四边形?并证明你的结论;
(3)若点E是直线AB上一点,平面内存在一点F,使得四边形CBEF是正方形,求点E的坐标,请直接写出答案.

【答案】(1)![]() (-9,0);(2)四边形ABCD是矩形;(3)(-2,-4),(10,4)
(-9,0);(2)四边形ABCD是矩形;(3)(-2,-4),(10,4)
【解析】(1)根据,直线![]() 与直线
与直线![]() 平行,设出
平行,设出![]() 的函数关系式,再利用待定系数法即可求出
的函数关系式,再利用待定系数法即可求出![]() 的函数关系式,再令
的函数关系式,再令![]() ,即可求出点D坐标;
,即可求出点D坐标;
(2)利用平面内两点间的距离公式求出AD与BC的长相等,再根据AD∥BC及BD=AC,即可求出结论;
(3)根据正方形的判定,作出图形,即可得出点E的坐标.
详解:(1)∵直线![]() 与直线
与直线![]() :
:![]() 平行,
平行,
∴设![]() ,
,
∵直线![]() 经过点
经过点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 时,
时,
![]() ,
,
解得![]() ,
,
∴![]() .
.
(2)四边形ABCD是矩形.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵AD∥BC,
∴四边形ABCD是平行四边形,
∵![]() ,
,![]() ,
,
∴BD=AC,
∴平行四边形ABCD是矩形.
(3)如图所示,
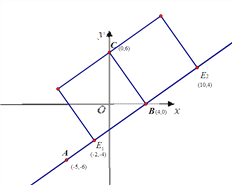
点E坐标为:![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教师节当天,出租车司机小王在东西向的街道上免费接送教师,规定向东为正,向西为负,当天出租车的行程如下(单位:千米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 将最后一名老师送到目的地时,小王距出发地多少千米?方位如何?
将最后一名老师送到目的地时,小王距出发地多少千米?方位如何?
![]() 若汽车耗油量为
若汽车耗油量为![]() 升/千米,则当天耗油多少升?若汽油价格为
升/千米,则当天耗油多少升?若汽油价格为![]() 元/升,则小王共花费了多少元钱?
元/升,则小王共花费了多少元钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,则∠A、∠C、∠E、∠F满足的数量关系是( )

A. ∠A=∠C+∠E+∠F B. ∠A+∠E﹣∠C﹣∠F=180°
C. ∠A﹣∠E+∠C+∠F=90° D. ∠A+∠E+∠C+∠F=360°
查看答案和解析>>
科目:初中数学 来源: 题型:
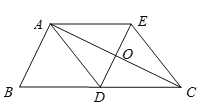
【题目】如图,已知△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,联结EC.
(1)求证:四边形ADCE是平行四边形;
(2)当∠BAC=90°时,求证:四边形ADCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
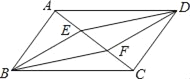
【题目】如图,在□ABCD中,E,F是对角线AC上的两点且AE=CF,在①BE=DF;②BE∥DF;③AB=DE;④四边形EBFD为平行四边形;⑤S△ADE=S△ABE;⑥AF=CE这些结论中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,CA=CB=4,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°、∠MPN=30°)按如图所示放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.
(1)当PN∥BC时,∠ACP=_____度.
(2)在点P滑动的过程中,当AP长度为多少时,△ADP与△BPC全等.
(3)在点P的滑动过程中,△PCD的形状可以是等腰三角形吗?若不可以,请说明理由;若可以,请求出夹角α的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题: 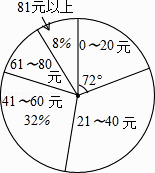
捐款 | 人数 |
0~20元 | |
21~40元 | |
41~60元 | |
61~80元 | 6 |
81元以上 | 4 |
(1)全班有多少人捐款?
(2)如果捐款0~20元的人数在扇形统计图中所占的圆心角为72°,那么捐款21~40元的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
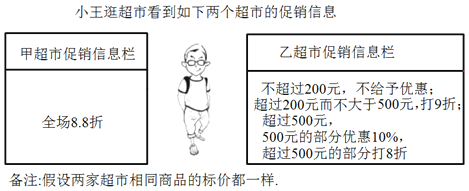
【题目】(1)当一次性购物标价总额是300元时,甲、乙超市实付款分别是多少?
(2)当标价总额是多少时,甲、乙超市实付款一样?
(3)小王两次到乙超市分别购物付款198元和466元,若他只去一次该超市购买同样多的商品,可以节省多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com