
【题目】工厂准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)工厂准备购进这两种型号的节能灯共50只,且A型节能灯的数量不多于B型节能灯数量的4倍,如何购买A、B型节能灯,可以使总费用最少,且总费用最少是多少.
【答案】(1)A型5元,B型7元;(2)A型40只,B型10只,总费用270元.
【解析】
(1)设一只A型节能灯的售价是x元,一只B型节能灯的售价是y元,根据:“1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元”列方程组求解即可;
(2)首先根据“A型节能灯的数量不多于B型节能灯数量的4倍”确定自变量的取值范围,然后得到有关总费用和A型灯的只数之间的关系得到函数解析式,确定函数的最值即可.
解:(1)设一只A型节能灯的售价是x元,一只B型节能灯的售价是y元,
根据题意,得:![]() ,解得:
,解得:![]() ,
,
(2)设购进A型节能灯a只,则购进B型节能灯(50-a)只,
总费用为:![]() ,
,
∵且A型节能灯的数量不多于B型节能灯数量的4倍,即![]() ,
,
解得:![]() ,
,
而a为正整数,
∴当a=40时,总费用最少,总费用为:-80+350=270元,
∴购进B型节能灯(50-a)=50-40=10只.


科目:初中数学 来源: 题型:
【题目】如图,![]() 是☉
是☉![]() 的直径,
的直径,![]() 为☉
为☉![]() 上一点,
上一点,![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() 两点,过点
两点,过点![]() 的切线交射线
的切线交射线![]() 于点
于点![]() .
.
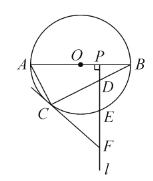
(1)求证:![]() .
.
(2)当![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,判断以
,判断以![]() 为顶点的四边形是什么特殊四边形,并说明理由;
为顶点的四边形是什么特殊四边形,并说明理由;
②若![]() ,且
,且![]() ,则
,则![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
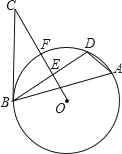
【题目】如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,BC=8,求弦BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 中,
中,![]() 是
是![]() 边上一点,
边上一点,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 的延长线于
的延长线于![]() ,且
,且![]() ,连接
,连接![]() .
.
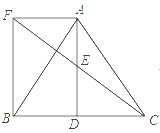
(1)求证:![]() 是
是![]() 的中点;
的中点;
(2)若![]() ,试判断四边形
,试判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,其中正确的结论分别是___.
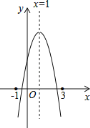
查看答案和解析>>
科目:初中数学 来源: 题型:
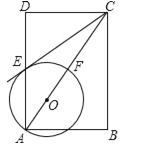
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
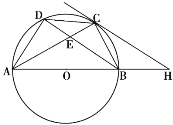
【题目】如图,点A,B,C,D是直径为AB的⊙O上四个点,C是劣弧![]() 的中点,AC交BD于点E,AE=2,EC=1.
的中点,AC交BD于点E,AE=2,EC=1.
(1)求证:△DEC∽△ADC;
(2)连结DO,探究四边形OBCD是否是菱形?若是,请你给予证明;若不是,请说明理由;
(3)延长AB到H,使BH=OB,求证:CH是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车早晨7∶00出发,从甲地驶往乙地送货.如图是货车行驶路程y(km)与行驶时间x(h)的完整的函数图像(其中点B、C、D在同一条直线上),小明研究图像得到了以下结论:
①甲乙两地之间的路程是100 km;
②前半个小时,货车的平均速度是40 km/h;
③8∶00时,货车已行驶的路程是60 km;
④最后40 km货车行驶的平均速度是100 km/h;
⑤货车到达乙地的时间是8∶24,
其中,正确的结论是( )

A.①②③④B.①③⑤C.①③④D.①③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com