
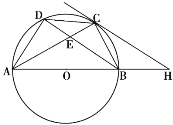
【题目】如图,点A,B,C,D是直径为AB的⊙O上四个点,C是劣弧![]() 的中点,AC交BD于点E,AE=2,EC=1.
的中点,AC交BD于点E,AE=2,EC=1.
(1)求证:△DEC∽△ADC;
(2)连结DO,探究四边形OBCD是否是菱形?若是,请你给予证明;若不是,请说明理由;
(3)延长AB到H,使BH=OB,求证:CH是⊙O的切线.
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D为BC边上一点,DC=2BD=4,以点D为顶点作正方形DEFG,且DE=BC,连接AE,AG.若将正方形DEFG绕D点旋转一周,当AE取最小值时,AG的长为____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)工厂准备购进这两种型号的节能灯共50只,且A型节能灯的数量不多于B型节能灯数量的4倍,如何购买A、B型节能灯,可以使总费用最少,且总费用最少是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛.为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”.根据调查结果绘制成的统计图(部分)如图所示:大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表:
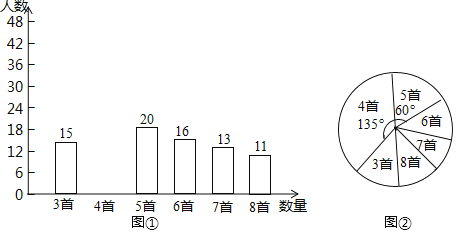
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 10 | 10 | 15 | 40 | 25 | 20 |
请根据调查的信息
(1)以抽查的这部分学生为样本,求“在大赛启动之初,一周诗词诵背数量不超过5首”的概率;
(2)以这部分学生经典诗词大赛启动之初和结束一个月后,一周诗词诵背数量的平均数作为决策依据,说明平均每名学生一周诗词诵背数量的增长率接近16%还是22%?
查看答案和解析>>
科目:初中数学 来源: 题型:
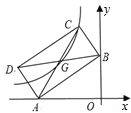
【题目】如图,矩形ABCD的两个顶点A、B分别在x、y轴上,顶点C、D位于第二象限,且OA=3,OB=2,对角线AC、BD交于点G,若双曲线![]() 经过C、G,则k=__________.
经过C、G,则k=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD的三个顶点坐标是A(﹣9,0)、B(﹣3,0)、C(0,4).若某反比例函数的图象经过线段CD的中点,则其解析式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
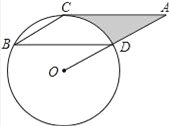
【题目】如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,![]() .
.
(1)试说明:AC是⊙O的切线;
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
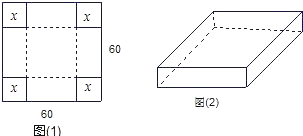
【题目】用一块边长为60㎝的正方形薄钢片制作一个长方体盒子:如果要做成一个没有盖的长方体盒子,可先在薄钢片的四个角上截去四个相同的小正方形,如图(1),然后把四边折合起来,如图(2)
(1)求做成的盒子底面积y(㎝2)与截去小正方形边长x(㎝)之间的函数关系式;
(2)当做成的盒子的底面积为900㎝2时,试求该盒子的容积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com