
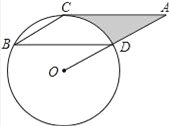
【题目】如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,![]() .
.
(1)试说明:AC是⊙O的切线;
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接OC,根据圆周角定理求出∠COA,根据三角形内角和定理求出∠OCA,根据切线的判定推出即可.
(2)求出DE,解直角三角形求出OC,分别求出△ACO的面积和扇形COD的面积根据转换思想,由即![]() 可得出答案.
可得出答案.
试题解析:解:(1)证明:如答图,连接OC,交BD于E,
∵∠B和∠COD是同弧所对的圆周角和圆心角,∴∠COD=2∠B.
∵∠B=30°,∴∠COD=60°.
∵∠A=30°,∴∠OCA=90°,即OC⊥AC.∴AC是⊙O的切线.
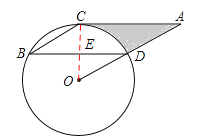
(2)∵AC∥BD,∠OCA=90°,∴∠OED=∠OCA=90°.
∵BD=![]() ,∴
,∴![]() .
.
∵在Rt△ODE中, ![]() ,∴OD=2.
,∴OD=2.
∵在Rt△ACO中, ![]() , ∴AC=
, ∴AC=![]() .
.
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】关于函数y=﹣x+3,下列结论正确的是( )
A. 它的图象必经过点(1,1) B. 它的图象经过第一、二、三象限
C. 它的图象与y轴的交点坐标为(0,3) D. y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
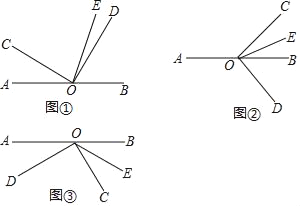
【题目】如图①,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)若∠AOC=30°时,则∠DOE的度数为_____;
(2)将图①中的∠COD绕顶点O顺时针旋转至图②的位置,其它条件不变,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
(3)将图①中的∠COD绕顶点O顺时针旋转至图③的位置,其他条件不变.直接写出∠AOC和∠DOE的度数之间的关系:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 近似数1.8与1.80表示的意义不同 B. 0.0200精确到万分位
C. 2.0万精确到万位 D. 1.0×104精确到千位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国“一带一路”战略给沿线国家和地区带来很大的经济效益,沿线某地区居民2015年年收入200美元,预计2017年年收入将达到1000美元,设2015年到2017年该地区居民年人均收入平均增长率为x,可列方程为( )
A. 200(1+2x)=1000B. 200+2x=1000
C. 200(1+x2)=1000D. 200(1+x)2=1000
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=C,试猜想a,b,c之间的一种关系,并给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a1、a2、a3、a4、…满足下列条件:a1=﹣1,a2=﹣|a1+2|,a3=﹣|a2+3|,a4=﹣|a3+4|,…,an+1=﹣|an+n+1|(n为正整数)依此类推,则a2019的值为( )
A. ﹣1009B. ﹣1010C. ﹣2019D. ﹣2020
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com