
【题目】平行四边形ABCD的三个顶点坐标是A(﹣9,0)、B(﹣3,0)、C(0,4).若某反比例函数的图象经过线段CD的中点,则其解析式为_____.
【答案】y=![]() 或y=﹣
或y=﹣![]() .
.
【解析】
分三种情况确定平行四边形的顶点D;![]() 当ABCD时平行四边形时,CD的中点为
当ABCD时平行四边形时,CD的中点为![]() ;
;![]() 当ABDC为平行四边形时,CD的中点为
当ABDC为平行四边形时,CD的中点为![]() ,
,![]() 当ACBC是平行四边形时,CD的中点为
当ACBC是平行四边形时,CD的中点为![]() ;由中点坐标可求反比例函数的解析式.
;由中点坐标可求反比例函数的解析式.
解:如图:
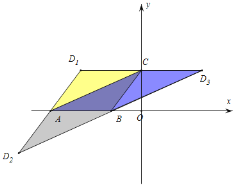
∵A(﹣9,0)、B(﹣3,0)、C(0,4),
∴AB=6,BC=5,
设反比例函数为y=![]() ,
,
①当ABCD时平行四边形时,
∵AB=CD,![]() ,
,
∴D(﹣6,4),
∴CD的中点为(﹣3,4),
∴k=﹣12,
∴y=﹣![]() ;
;
②当ABDC为平行四边形时,
∵AB=CD,![]() ,
,
∴D(6,4),
∴CD的中点为(3,4),
∴k=12,
∴y=![]() ;
;
③当ACBC是平行四边形时,
∴![]() ,BC=AD,
,BC=AD,
此时CD的中点与AB的中点相同,
∴CD的中点为(﹣6,0),
∴k=0,不符合题意;
综上所述:反比例函数的解析式为y=![]() 或y=﹣
或y=﹣![]() ;
;
故答案为y=![]() 或y=﹣
或y=﹣![]() .
.


 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
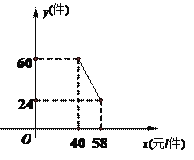
【题目】国家支持大学生创新办实业,提供小额无息贷款,学生王亮享受国家政策贷款36000元用于代理某品牌服装销售,已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图中的一条线段(实线)来表示.该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含贷款).
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)若该店暂不考虑偿还贷款,当某天的销售价为48元/件时,当天正好收支平衡(销售额-成本=支出),求该店员工的人数;
(3)若该店只有2名员工,则该店至少需要多少天能还清所有贷款?此时每件服装的价格应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
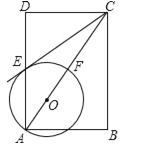
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
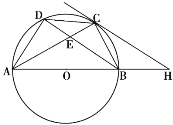
【题目】如图,点A,B,C,D是直径为AB的⊙O上四个点,C是劣弧![]() 的中点,AC交BD于点E,AE=2,EC=1.
的中点,AC交BD于点E,AE=2,EC=1.
(1)求证:△DEC∽△ADC;
(2)连结DO,探究四边形OBCD是否是菱形?若是,请你给予证明;若不是,请说明理由;
(3)延长AB到H,使BH=OB,求证:CH是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=﹣m与y轴交于点A,直线a:y=x+m与y轴交于点B,抛物线y=x2+mx的顶点为C,且与x轴左交点为D(其中m>0).
(1)当AB=12时,在抛物线的对称轴上求一点P使得△BOP的周长最小;
(2)当点C在直线l上方时,求点C到直线l距离的最大值;
(3)若把横坐标、纵坐标都是整数的点称为“整点”.当m=2020时,求出在抛物线和直线a所围成的封闭图形的边界上的“整点”的个数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为_____.
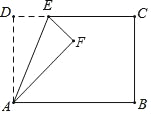
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE,动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某点Q1向终点Q2匀速运动,它们同时到达终点.
分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE,动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某点Q1向终点Q2匀速运动,它们同时到达终点.
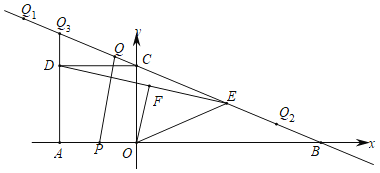
(1)求点B的坐标和OE的长;
(2)设点Q2为(m,n),当![]() tan∠EOF时,求点Q2的坐标;
tan∠EOF时,求点Q2的坐标;
(3)根据(2)的条件,当点P运动到AO中点时,点Q恰好与点C重合.
①延长AD交直线BC于点Q3,当点Q在线段Q2Q3上时,设Q3Q=s,AP=t,求s关于t的函数表达式.
②当PQ与△OEF的一边平行时,求所有满足条件的AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】刘徵是我国古代最杰出的数学家之一,他在《九算术圆田术)中用“割圆术”证明了圆面积的精确公式,并给出了计算圆周率的科学方法(注:圆周率=圆的周长与该圆直径的比值)“割圆术”就是以“圆内接正多边形的面积”,来无限逼近“圆面积”,刘徽形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣.刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径R.此时圆内接正六边形的周长为6R,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为_____.(参考数据:sinl5°=0.26)
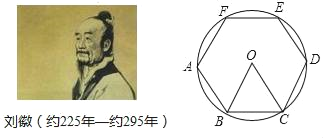
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com