
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯп![]() ЗжБ№НЛxжсЁЂyжсгкЕуBЃЌCЃЌе§ЗНаЮAOCDЕФЖЅЕуDдкЕкЖўЯѓЯоФкЃЌEЪЧBCжаЕуЃЌOFЁЭDEгкЕуFЃЌСЌНсOEЃЌЖЏЕуPдкAOЩЯДгЕуAЯђжеЕуOдШЫйдЫЖЏЃЌЭЌЪБЃЌЖЏЕуQдкжБЯпBCЩЯДгФГЕуQ1ЯђжеЕуQ2дШЫйдЫЖЏЃЌЫќУЧЭЌЪБЕНДяжеЕуЃЎ
ЗжБ№НЛxжсЁЂyжсгкЕуBЃЌCЃЌе§ЗНаЮAOCDЕФЖЅЕуDдкЕкЖўЯѓЯоФкЃЌEЪЧBCжаЕуЃЌOFЁЭDEгкЕуFЃЌСЌНсOEЃЌЖЏЕуPдкAOЩЯДгЕуAЯђжеЕуOдШЫйдЫЖЏЃЌЭЌЪБЃЌЖЏЕуQдкжБЯпBCЩЯДгФГЕуQ1ЯђжеЕуQ2дШЫйдЫЖЏЃЌЫќУЧЭЌЪБЕНДяжеЕуЃЎ
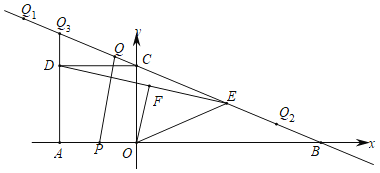
ЃЈ1ЃЉЧѓЕуBЕФзјБъКЭOEЕФГЄЃЛ
ЃЈ2ЃЉЩшЕуQ2ЮЊ(mЃЌn)ЃЌЕБ![]() tanЁЯEOFЪБЃЌЧѓЕуQ2ЕФзјБъЃЛ
tanЁЯEOFЪБЃЌЧѓЕуQ2ЕФзјБъЃЛ
ЃЈ3ЃЉИљОнЃЈ2ЃЉЕФЬѕМўЃЌЕБЕуPдЫЖЏЕНAOжаЕуЪБЃЌЕуQЧЁКУгыЕуCжиКЯЃЎ
ЂйбгГЄADНЛжБЯпBCгкЕуQ3ЃЌЕБЕуQдкЯпЖЮQ2Q3ЩЯЪБЃЌЩшQ3QЃНsЃЌAPЃНtЃЌЧѓsЙигкtЕФКЏЪ§БэДяЪНЃЎ
ЂкЕБPQгыЁїOEFЕФвЛБпЦНааЪБЃЌЧѓЫљгаТњзуЬѕМўЕФAPЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈ8ЃЌ0ЃЉЃЌ![]() ЃЛЃЈ2ЃЉЃЈ6ЃЌ1ЃЉЃЛЃЈ3ЃЉЂй
ЃЛЃЈ2ЃЉЃЈ6ЃЌ1ЃЉЃЛЃЈ3ЃЉЂй![]() ЃЌЂк
ЃЌЂк![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉСюyЃН0ЃЌПЩЕУBЕФзјБъЃЌРћгУЙДЙЩЖЈРэПЩЕУBCЕФГЄЃЌМДПЩЕУЕНOEЃЛ
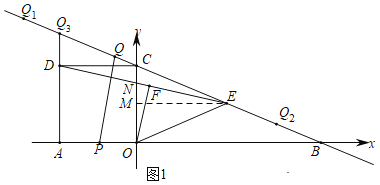
ЃЈ2ЃЉШчЭМЃЌзїИЈжњЯпЃЌжЄУїЁїCDNЁзЁїMENЃЌЕУCNЃНMNЃН1ЃЌМЦЫуENЕФГЄЃЌИљОнУцЛ§ЗЈПЩЕУOFЕФГЄЃЌРћгУЙДЙЩЖЈРэЕУOFЕФГЄЃЌгЩ![]() КЭ
КЭ![]() ЃЌПЩЕУНсТлЃЛ
ЃЌПЩЕУНсТлЃЛ
ЃЈ3ЃЉЂйЯШЩшsЙигкtГЩвЛДЮКЏЪ§ЙиЯЕЃЌЩшsЃНktЃЋbЃЌИљОнЕБЕуPдЫЖЏЕНAOжаЕуЪБЃЌЕуQЧЁКУгыЕуCжиКЯЃЌЕУtЃН2ЪБЃЌCDЃН4ЃЌDQ3ЃН2ЃЌsЃН![]() ЃЌИљОнQ3ЃЈ4ЃЌ6ЃЉЃЌQ2ЃЈ6ЃЌ1ЃЉЃЌПЩЕУtЃН4ЪБЃЌsЃН
ЃЌИљОнQ3ЃЈ4ЃЌ6ЃЉЃЌQ2ЃЈ6ЃЌ1ЃЉЃЌПЩЕУtЃН4ЪБЃЌsЃН![]() ЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЕУsЙигкtЕФКЏЪ§БэДяЪНЃЛ
ЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЕУsЙигкtЕФКЏЪ§БэДяЪНЃЛ
ЂкЗжШ§жжЧщПіЃК
ЃЈiЃЉЕБPQЁЮOEЪБЃЌИљОн![]() ЃЌБэЪОBHЕФГЄЃЌИљОнABЃН12ЃЌСаЗНГЬПЩЕУtЕФжЕЃЛ
ЃЌБэЪОBHЕФГЄЃЌИљОнABЃН12ЃЌСаЗНГЬПЩЕУtЕФжЕЃЛ
ЃЈiiЃЉЕБPQЁЮOFЪБЃЌИљОнtanЁЯHPQЃНtanЁЯCDNЃН![]() ЃЌСаЗНГЬЮЊ2t2ЃН
ЃЌСаЗНГЬЮЊ2t2ЃН![]() (7
(7![]() t)ЃЌПЩЕУtЕФжЕЃЎ
t)ЃЌПЩЕУtЕФжЕЃЎ
ЃЈiiiЃЉгЩЭМаЮПЩжЊPQВЛПЩФмгыEFЦНааЃЎ
НтЃКЃЈ1ЃЉСю![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЮЊ
ЮЊ![]() .
.
Ёп![]() ЮЊ
ЮЊ![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ![]() .
.
гжЁп![]() ЮЊ
ЮЊ![]() жаЕуЃЌЁр
жаЕуЃЌЁр![]() .
.
ЃЈ2ЃЉШчЭМЃЌзї![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() .
.
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
гЩЙДЙЩЖЈРэЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() .
.
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЮЊ
ЮЊ![]() .
.
ЃЈ3ЃЉЂйЁпЖЏЕу![]() ЭЌЪБзїдШЫйжБЯпдЫЖЏЃЌ
ЭЌЪБзїдШЫйжБЯпдЫЖЏЃЌ
Ёр![]() Йигк
Йигк![]() ГЩвЛДЮКЏЪ§ЙиЯЕЃЌЩш
ГЩвЛДЮКЏЪ§ЙиЯЕЃЌЩш![]() ЃЌ
ЃЌ
НЋ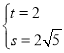 КЭ
КЭ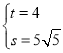 ДњШыЕУ
ДњШыЕУ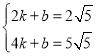 ЃЌНтЕУ
ЃЌНтЕУ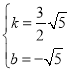 ЃЌ
ЃЌ
Ёр![]() .
.
ЂкЃЈЂЁЃЉЕБ![]() ЪБЃЌЃЈШчЭМЃЉЃЌ
ЪБЃЌЃЈШчЭМЃЉЃЌ![]() ЃЌ
ЃЌ
зї![]() жсгкЕу
жсгкЕу![]() ЃЌдђ
ЃЌдђ![]() .
.
Ёп![]()
![]() ЃЌ
ЃЌ
гжЁп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() .
.
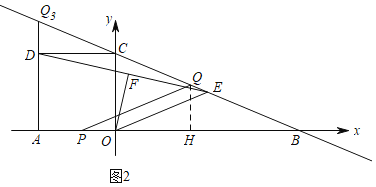
ЃЈЂЂЃЉЕБ![]() ЪБЃЈШчЭМЃЉЃЌЙ§Еу
ЪБЃЈШчЭМЃЉЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌгЩ
ЃЌгЩ![]() ЕУ
ЕУ![]() .
.
Ёп![]() ,
,
Ёр![]() ,
,
Ёр![]()
![]() ЃЌ
ЃЌ
Ёр![]() .
.
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() .
.
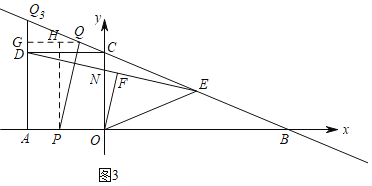
ЃЈЂЃЃЉгЩЭМаЮПЩжЊ![]() ВЛПЩФмгы
ВЛПЩФмгы![]() ЦНаа.
ЦНаа.
злЩЯЫљЪіЃЌЕБ![]() гы
гы![]() ЕФвЛБпЦНааЪБЃЌ
ЕФвЛБпЦНааЪБЃЌ![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() Лђ
Лђ![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃЌЁЯBACЃН100ЁуЃЌдкЭЌвЛЦНУцФкЃЌНЋЁїABCШЦЕуAЫГЪБеыа§зЊЕНЁїAB1C1ЕФЮЛжУЃЌСЌНгBB1ЃЌШєBB1ЁЮAC1ЃЌдђЁЯCAC1ЕФЖШЪ§ЪЧЃЈЁЁЁЁЃЉ
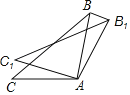
A.10ЁуB.20ЁуC.30ЁуD.40Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦНааЫФБпаЮABCDЕФШ§ИіЖЅЕузјБъЪЧAЃЈЉ9ЃЌ0ЃЉЁЂBЃЈЉ3ЃЌ0ЃЉЁЂCЃЈ0ЃЌ4ЃЉЃЎШєФГЗДБШР§КЏЪ§ЕФЭМЯѓОЙ§ЯпЖЮCDЕФжаЕуЃЌдђЦфНтЮіЪНЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() ЕФЖдГЦжсЪЧжБЯп
ЕФЖдГЦжсЪЧжБЯп![]() ЃЌгы
ЃЌгы![]() жсНЛгк
жсНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЮЊХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§Еу
ЮЊХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕу![]() дкЕквЛЯѓЯоФкЃЌЕБ
дкЕквЛЯѓЯоФкЃЌЕБ![]() ЪБЃЌЧѓЫФБпаЮ
ЪБЃЌЧѓЫФБпаЮ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ3ЃЉНЋ![]() ШЦЦНУцжБНЧзјБъЯЕжаФГЕуФцЪБеыа§зЊ
ШЦЦНУцжБНЧзјБъЯЕжаФГЕуФцЪБеыа§зЊ![]() ЃЌЖдгІЕуЮЊ
ЃЌЖдгІЕуЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕБ
ЃЌЕБ![]() жагаСНИіЖЅЕуТфдкХзЮяЯпЩЯЪБЃЌжБНгаДГі
жагаСНИіЖЅЕуТфдкХзЮяЯпЩЯЪБЃЌжБНгаДГі![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯжШчНёЃЌЁАРЌЛјЗжРрЁБвтЪЖвбЩюШыШЫаФЃЌРЌЛјвЛАуПЩЗжЮЊЃКПЩЛиЪеЮяЁЂГјгрРЌЛјЁЂгаКІРЌЛјЁЂЦфЫќРЌЛјЃЎЦфжаМзФУСЫвЛДќРЌЛјЃЌввФУСЫСНДќРЌЛјЃЎ
ЃЈ1ЃЉжБНгаДГіМзЫљФУЕФРЌЛјЧЁКУЪЧЁАГјгрРЌЛјЁБЕФИХТЪЃЛ
ЃЈ2ЃЉЧѓввЫљФУЕФСНДќРЌЛјВЛЭЌРрЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
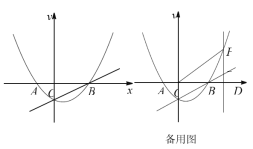
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпy=Љx2+mx+nНЛxжсгкЕуAЃЈЉ2ЃЌ0ЃЉКЭЕуBЃЌНЛyжсгкЕуCЃЈ0ЃЌ2ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШєЕуMдкХзЮяЯпЩЯЃЌЧвSЁїAOM=2SЁїBOCЃЌЧѓЕуMЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЩшЕуNЪЧЯпЖЮACЩЯЕФвЛЖЏЕуЃЌзїDNЁЭxжсЃЌНЛХзЮяЯпгкЕуDЃЌЧѓЯпЖЮDNГЄЖШЕФзюДѓжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЦНУцжБНЧзјБъЯЕ![]() жаЃЌжБЯп
жаЃЌжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() ЯрНЛгк
ЯрНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЈЕу
СНЕуЃЈЕу![]() дкЕу
дкЕу![]() ЕФзѓВрЃЉЃЌгыХзЮяЯп
ЕФзѓВрЃЉЃЌгыХзЮяЯп![]() ЕФЖдГЦжсЯрНЛгкЕу
ЕФЖдГЦжсЯрНЛгкЕу![]() ЃЌМЧХзЮяЯп
ЃЌМЧХзЮяЯп![]() ЕФЖЅЕуЮЊ
ЕФЖЅЕуЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсЃЌДЙзуЮЊ
жсЃЌДЙзуЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШє![]() жсЃЌ
жсЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЕБ![]() ЃЌХзЮяЯп
ЃЌХзЮяЯп![]() гы
гы![]() жсНЛгк
жсНЛгк![]() ЪБЃЌЩшЩфЯп
ЪБЃЌЩшЩфЯп![]() гыжБЯп
гыжБЯп![]() ЯрНЛгк
ЯрНЛгк![]() ЕуЃЌЧѓ
ЕуЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉбгГЄ![]() ЃЌ
ЃЌ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЧѓжЄЃКЫФБпаЮ
ЃЌЧѓжЄЃКЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЎ
ЪЧЦНааЫФБпаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЕу![]() ЗжБ№ЪЧБпГЄЮЊ4cmЕФЕШБпШ§НЧаЮ
ЗжБ№ЪЧБпГЄЮЊ4cmЕФЕШБпШ§НЧаЮ![]() Бп
Бп![]() ЖЏЕуЃЌЕу
ЖЏЕуЃЌЕу![]() ДгЖЅЕу
ДгЖЅЕу![]() би
би![]() ЯђЕу
ЯђЕу![]() дЫЖЏЃЌЕу
дЫЖЏЃЌЕу![]() ЭЌЪБДгЖЅЕу
ЭЌЪБДгЖЅЕу![]() би
би![]() Яђ
Яђ![]() дЫЖЏЃЌЫќУЧЕФЫйЖШЖМЪЧ
дЫЖЏЃЌЫќУЧЕФЫйЖШЖМЪЧ![]() ЃЌЕБЕНДяжеЕуЪБЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЌСЌНг
ЃЌЕБЕНДяжеЕуЪБЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЌСЌНг![]() НЛгкЕуMЃЎ
НЛгкЕуMЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕу![]() дкдЫЖЏЕФЙ§ГЬжаЃЌ
дкдЫЖЏЕФЙ§ГЬжаЃЌ![]() БфЛЏТ№ЃПШєБфЛЏЃЌЧыЫЕУїРэгЩЃЌШєВЛБфЃЌдђЧѓГіЫќЕФЖШЪ§ЃЛ
БфЛЏТ№ЃПШєБфЛЏЃЌЧыЫЕУїРэгЩЃЌШєВЛБфЃЌдђЧѓГіЫќЕФЖШЪ§ЃЛ
ЃЈ3ЃЉЕБ![]() ЮЊКЮжЕЪБ
ЮЊКЮжЕЪБ![]() ЪЧжБНЧШ§НЧаЮЃП
ЪЧжБНЧШ§НЧаЮЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЕШбќ![]() жаЃЌ
жаЃЌ![]() ЃЌзї
ЃЌзї![]() ЕФЦНЗжЯпНЛ
ЕФЦНЗжЯпНЛ![]() гкЕу
гкЕу![]() ЃЌНЋ
ЃЌНЋ![]() ШЦЕу
ШЦЕу![]() а§зЊЃЌЪЙ
а§зЊЃЌЪЙ![]() ЕФСНБпНЛжБЯп
ЕФСНБпНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЕБ![]() ШЦЕу
ШЦЕу![]() а§зЊЕНШчЭМЂйЕФЮЛжУЪБЃЌЧыжБНгаДГіШ§ЬѕЯпЖЮ
а§зЊЕНШчЭМЂйЕФЮЛжУЪБЃЌЧыжБНгаДГіШ§ЬѕЯпЖЮ![]() ЕФЪ§СПЙиЯЕЃЛ
ЕФЪ§СПЙиЯЕЃЛ
ЃЈ2ЃЉЕБ![]() ШЦЕу
ШЦЕу![]() а§зЊЕНШчЭМЂкЕФЮЛжУЪБЃЌЃЈ1ЃЉжаНсТлЪЧЗёГЩСЂЃЌШєГЩСЂЃЌЧыжЄУїЃЛШєВЛГЩСЂЃЌЧыаДГіе§ШЗЕФНсТлЃЌВЂЫЕУїРэгЩЃЛ
а§зЊЕНШчЭМЂкЕФЮЛжУЪБЃЌЃЈ1ЃЉжаНсТлЪЧЗёГЩСЂЃЌШєГЩСЂЃЌЧыжЄУїЃЛШєВЛГЩСЂЃЌЧыаДГіе§ШЗЕФНсТлЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШє![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌЧыжБНгаДГіЯпЖЮ
ЪБЃЌЧыжБНгаДГіЯпЖЮ![]() ЕФГЄЖШЃЎ
ЕФГЄЖШЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com