
【题目】如图,已知二次函数![]() 的图象经过A(3,0),B(0,1),C(2,2)三点.
的图象经过A(3,0),B(0,1),C(2,2)三点.
(1)求二次函数![]() 的解析式;
的解析式;
(2)设点D(![]() ,m )在二次函数的图象上,将∠ACB绕点C按顺时针方向旋转至∠FCE,使得射线CE与
,m )在二次函数的图象上,将∠ACB绕点C按顺时针方向旋转至∠FCE,使得射线CE与![]() 轴的正半轴交于点E,且经过点D,射线CF与线段OA交于点F.求证:BE=2FO;
轴的正半轴交于点E,且经过点D,射线CF与线段OA交于点F.求证:BE=2FO;
(3)是否存在点H(n,2),使得点A、D、H构成的△ADH是直角三角形?若存在,有几个符合条件的点H?(直接回答,不必说明理由)

【答案】(1)二次函数的解析式为![]() ;
;
(2)证明见解析;
(3)存在4个符合条件的点H,使得点A、D、H构成的△ADH是直角三角形.
【解析】(1)用待定系数法求出抛物线解析式即可;(2)证明Rt△NBC≌Rt△MAC和△ACF≌△BCE, 得出AF=BE,然后利用一次函数求出BE=2FO;(3)最后直接求出符合条件△ADH是直角三角形的点H.
(1)解:把A(3,0),B(0,1),C(2,2)代入![]() ,
,
得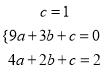 ∴
∴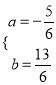

∴二次函数的解析式为![]() .
.
(2)过点C作CM⊥OA于点M,CN⊥y轴于点N,

∵A(3,0),B(0,1),C(2,2),
∴CM= CN=2,CA=CB=![]() ,
, ![]()
∴Rt△NBC≌Rt△MAC,
∴∠CAF=∠CBE,
∵将∠ACB绕点C按顺时针方向旋转至∠FCE,
∴∠FCE=∠ACB,
∴∠FCE-∠BCF=∠ACB-∠BCF,
即∠ACF=∠BCE,
又∵CB=CA,∴△ACF≌△BCE,
∴AF=BE.
∵二次函数的解析式为![]() ,
,
当![]() 时,
时, ![]() ,∴
,∴![]()
设直线CD: ![]() ,把C(2,2)、
,把C(2,2)、![]() 代入得
代入得
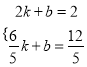 , 解得
, 解得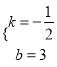 ,
,
∴直线CD: ![]() .
.
∴E(0,3),BE=2, ∴AF=BE=2 ,
∴FO=OA-AF=1.
∴BE=2FO.
(3)存在4个符合条件的点H,使得点A、D、H构成的△ADH是直角三角形.
“点睛”本题考查了二次函数的综合题,熟练掌握运用待定系数法求函数解析式;熟练掌握二次函数图象上点的坐标特征,根据题意利用一次函数求出BE=2FO是解答此题的关键.


科目:初中数学 来源: 题型:
【题目】某市出租车收费标准:3 km以内(含3 km)起步价为8元,超过3 km后每1 km加收1.8元.
(1)若小明坐出租车行驶了6 km,则他应付多少元车费?
(2)如果用s表示出租车行驶的路程,m表示出租车应收的车费,请你表示出s与m之间的数量关系(s>3).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将点(﹣1,3)向左平移2个单位,再向下平移4个单位得到点B,则B点坐标为( )
A. (﹣3,﹣1) B. (﹣1,﹣1) C. (﹣1,1) D. (﹣2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下面给出的数轴,解答下面的问题:
(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数A:_____B:_____.
(2)观察数轴,与点A的距离为4的点表示的数是:_____.
(3)若将数轴折叠,使得A点与﹣2表示的点重合,则B点与数_____表示的点重合.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:无论![]() 取何值,多项式:
取何值,多项式: ![]() 的值不变.请回答问题:
的值不变.请回答问题:
(1)请直接写出a、b、c的值: ![]() = ,
= , ![]() = ,
= , ![]() = ;
= ;
(2)数轴上![]() 三个数所对应的点分别为A、B、C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和4个单位长度的速度向右运动,假设
三个数所对应的点分别为A、B、C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和4个单位长度的速度向右运动,假设![]() 秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC.
秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC.
①![]() 秒钟过后,BC的长度为 (用含
秒钟过后,BC的长度为 (用含![]() 的关系式表示);
的关系式表示);
②请问:4AC﹣5AB的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级有5名教师带学生去公园秋游,公园的门票为每人30元,现有两种优惠方案,甲方案:带队教师免费,学生按8折收费;乙方案:师生都按7.5折收费.
(1)若有m名学生,则用式子表示两种优惠方案各需要多少元?
(2)当m为何值时,两种方案一样钱?(列方程计算)
(3)当m =100时,采用哪种方案优惠?优惠多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com