[题目]下列运算正确的是( )A.a2a3=a6B.a3÷a2=aC.(a3)2=a9D.a2+a3=a5 题目和参考答案——青夏教育精英家教网—

【题目】下列运算正确的是（）
A.a2a3=a6
B.a3÷a2=a
C.（a3）2=a9
D.a2+a3=a5

【答案】B
【解析】解：A、a2a3=a2+3=a5同底数幂的乘法，底数不变指数相加，故本选项错误； B、a3÷a2=a同底数幂的除法，底数不变指数相减，故本选项正确；
C、（a3）2=x6 ，幂的乘方，底数不变指数相乘，故本选项错误；
D、a2+a3=a5不能合并同类项，故本选项错误．
故选B．
【考点精析】关于本题考查的同底数幂的乘法和同底数幂的除法，需要了解同底数幂的乘法法则aman=am+n(m,n都是正数)；同底数幂的除法法则：am÷an=am-n（a≠0，m，n都是正整数，且m＞n）才能得出正确答案．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】某县九年级有15000名学生参加安全应急预案知识竞赛活动，为了了解本次知识竞赛的成绩分布情况，从中抽取了400名学生的得分（得分取正整数，满分100分）进行统计：

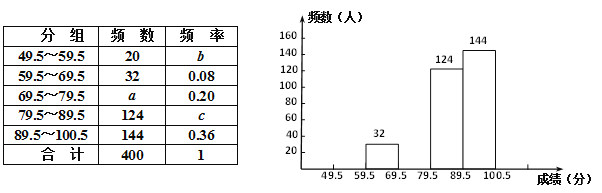
请结合图表完成下列问题：

（1）表中的，b= ， c= ；

（2）请把频数分布直方图补充完整；

（3）若将得分转化为等级，规定得分低于59.5分评为“D”，59.5～69.5分评为“C”，69.5～89.5分评为“B”，89.5～100.5分评为“A”，这次15000名学生中约有多少人被评为“B”？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】多边形的内角和与某一个外角的度数和为1350度．

(1)求多边形的边数；

(2)此多边形必有一内角为多少度？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】将矩形纸片OABC放在平面直角坐标系中,0为坐标原点,点A在y轴上,点C在x轴上,点B的坐标是(8,6),点P是边AB上的一个动点,将△OAP沿OP折叠，使点A落在点Q处.

(1)如图①，当点Q恰好落在OB上时.求点p的坐标；

(2)如图②，当点P是AB中点时,直线OQ交BC于M点.

①求证:MB=MQ；②求点Q的坐标.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在平面直角坐标系中，点A（0，4）、B（3，0），连接AB，将△AOB沿过点B的直线折叠，使点A落在x轴上的点A′处，折痕所在的直线交y轴正半轴于点C，则直线BC的解析式为（　　）

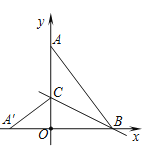
A. y=﹣x+ B. y=﹣x+ C. y=﹣x+ D. y=﹣2x+

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】若x1，x2是一元二次方程x2-2x-3=0的两个根，则x1，x2的值是（　　）

A. -1，-3 B. 1，3 C. 1，-3 D. -1，3

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在第37届中国洛阳文化节期间，某手工刺绣服装店老板某天销售了10件同款的女装上衣，销售尺码统计如下表：

尺码/cm	155	160	165	170	175
销量/件	1	4	2	2	1

则这10件上衣尺码的平均数和众数分别为（　　）

A.160，164B.160，4C.164，160D.164，4

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离，即|x|=|x﹣0|，也就是说|x|表示在数轴上数x与数0对应点之间的距离；这个结论可以推广为：|x﹣y|表示在数轴上数x、y对应点之间的距离；在解题中，我们常常运用绝对值的几何意义．

①解方程|x|=2，容易看出，在数轴上与原点距离为2的点对应的数为±2，即该方程的解为x=±2．

②在方程|x﹣1|=2中，x的值就是数轴上到1的距离为2的点对应的数，显然x=3或x=﹣1．

③在方程|x﹣1|+|x+2|=5中，显然该方程表示数轴上与1和﹣2的距离之和为5 的点对应的x值，在数轴上1和﹣2的距离为3，满足方程的x的对应点在1的右边或﹣2的左边．若x的对应点在1的右边，由图示可知，x=2；同理，若x的对应点在﹣2的左边，可得x=﹣3，所以原方程的解是x=2或x=﹣3．根据上面的阅读材料，解答下列问题：