
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=30cm.点P从点A出发,以1cm/s的速度向点D移动,点Q从点C出发,以3cm/s的速度向点B运动,点P和点Q分别从点A和点C同时出发,移动时间为ts.规定若其中一个动点先到达端点(终点)时,另一个动点也随之停止运动.
(1)求时间t的取值范围;
(2)当四边形ABQP为矩形时,求时间t的值;
(3)是否存在时间t的值,使得△APQ的面积是△ABC的面积的一半?若存在,请求出t的值,若不存在,说明理由.
【答案】
(1)解:点P停止的时间是24÷1=24s,点Q停止的时间是30÷3=10s,
所以时间t的取值范围是0≤t≤10
(2)解:由运动知,AP=t,CQ=3t,
∴BQ=30﹣3t,
若四边形ABQP是矩形.
∴AP=BQ.
即t=30﹣3t.
∴t=7.5.
(3)解:不存在.理由如下:
若△APQ的面积是△ABC的面积的一半时,
∴ ![]() AP×AB=
AP×AB= ![]() ×AB×BC.
×AB×BC.
∴t= ![]() ×30=15.
×30=15.
∵t的取值范围是0≤t≤10.
∴不存在t的值,使得使得△APQ的面积是△ABC的面积的一半.
【解析】(1)根据运动速度是距离即可得出结论;(2)有矩形的性质得出AP=BQ,建立方程求解即可得出结论;(3)假设△APQ的面积是△ABC的面积的一半,求出时间,判断是否在0≤t≤10内,即可得出结论.
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把抛物线y=2x2绕原点旋转180°,再向右平移1个单位,向下平移2个单位,所得的抛物线的函数表达式为( )
A.y=2(x﹣1)2﹣2B.y=2(x+1)2﹣2
C.y=﹣2(x﹣1)2﹣2D.y=﹣2(x+1)2﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:

(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD,对角线AC和BD相交于O,下面选项不能得出四边形ABCD是平行四边形的是( ) 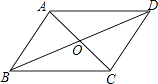
A.AB∥CD,且AB=CD
B.AB=CD,AD=BC
C.AO=CO,BO=DO
D.AB∥CD,且AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
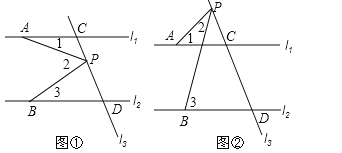
【题目】已知直线![]() ,直线
,直线![]() 与
与![]() 、
、![]() 分别交于C、D两点,点P是直线
分别交于C、D两点,点P是直线![]() 上的一动点.
上的一动点.
(1)如图,若动点P在线段CD之间运动(不与C、D两点重合),问在点P的运动过程中是否始终具有![]() 这一相等关系?试说明理由;
这一相等关系?试说明理由;
(2)如图,当动点P在线段CD之外且在![]() 的上方运动(不与C、D两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
的上方运动(不与C、D两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察图形,回答下列各题:
(1)图A中,共有____对对顶角;
(2)图B中,共有____对对顶角;
(3)图C中,共有____对对顶角;
(4)探究(1)--(3)各题中直线条数与对顶角对数之间的关系,若有n条直线相交于一点,则可形成________对对顶角;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com