
 抛物线y=-x2+6x-5与x轴交点为A,B(A在B左侧),顶点为D.与Y轴交于点C.
抛物线y=-x2+6x-5与x轴交点为A,B(A在B左侧),顶点为D.与Y轴交于点C.
| 4×5 |
| 2 |

| 4×4 |
| 2 |
| 4(m2-6m+5) |
| 2 |
| 14 |
| 14 |
| 14 |
| 14 |

|
|


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
 哈西客站投入使用以来,每天输送了大量的旅客.某日,从早8点开始到上午11点,为了缓解旅客压力,在原来基础上新增了3个售票窗口,每个售票窗口售出的车票数y(张)与售票时间x(小时)的关系满足如图所示的图象,其中OA为原有窗口,OB为新增窗口.
哈西客站投入使用以来,每天输送了大量的旅客.某日,从早8点开始到上午11点,为了缓解旅客压力,在原来基础上新增了3个售票窗口,每个售票窗口售出的车票数y(张)与售票时间x(小时)的关系满足如图所示的图象,其中OA为原有窗口,OB为新增窗口.查看答案和解析>>
科目:初中数学 来源: 题型:
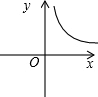 三角形的面积为6cm2,底边上的高y cm与底边长x cm之间的函数关系图象如图所示,问:
三角形的面积为6cm2,底边上的高y cm与底边长x cm之间的函数关系图象如图所示,问:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com