
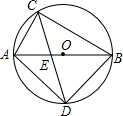
 如图,已知在⊙O中,直径AB为13cm,弦AC为5cm,∠ACB的平分线交⊙O于D,求BC,AD和BD的长.
如图,已知在⊙O中,直径AB为13cm,弦AC为5cm,∠ACB的平分线交⊙O于D,求BC,AD和BD的长. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
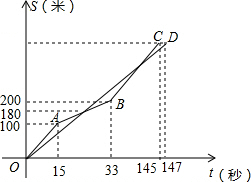 如图,在松雷中学学生跑步比赛中,甲、乙两学生跑步的路程s(米)与时间t(秒)之间的函数关系的图象分别为折线OABC和线段OD,下列说法正确的是( )
如图,在松雷中学学生跑步比赛中,甲、乙两学生跑步的路程s(米)与时间t(秒)之间的函数关系的图象分别为折线OABC和线段OD,下列说法正确的是( )| A、乙比甲先到终点 |
| B、比赛进行到29.4秒时,两人出发后第一次相遇 |
| C、乙测试的速度随时间增加而增大 |
| D、比赛全程甲的测试速度始终比乙的测试速度快 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
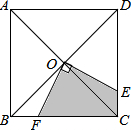 如图,正方形ABCD的对角线AC、BD的交点为O,点E、F分别在CD、BC边上,且∠EOF=90°.
如图,正方形ABCD的对角线AC、BD的交点为O,点E、F分别在CD、BC边上,且∠EOF=90°.查看答案和解析>>
科目:初中数学 来源: 题型:
 作图题:(不要求写作法)如图,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2.
作图题:(不要求写作法)如图,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com