
【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台.现将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.
两地区与该农机租赁公司商定的每天的租赁价格见下表:

(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说明有多少种分派方案,并将各种方案设计出来;
(3)如何分派才能使这50台联合收割机每天获得的租金最高?
【答案】(1)10≤x≤30(x是正整数);(2)有3种不同分配方案,当x=28时,即派往A地区甲型收割机2台,乙型收割机28台;派往B 地区甲型收割机18台,乙型收割机2台;当x=29时,即派往A地区甲型收割机1台,乙型收割机29台;派往B 地区甲型收割机19台,乙型收割机1台;
当x=30时,即30台乙型收割机全部派往A地区;20台甲型收割机全部派往B地区;(3)农机租赁公司将30台乙型收割机全部派往A地区;20台甲型收割要全部派往B地区,可使公司获得的租金最高.
【解析】(1)由派往A地区x台乙型联合收割机,则可知派往A地区有30-x台甲型联合收割机,派往B地区有30-x台乙型和x-10台甲型联合收割机,根据题意即可求得y与x间的函数关系式及x的取值范围;
(2)结合y与x间的函数关系式即可得到关于x的不等式,再根据x的取值范围即可得到x可能的取值,得到分配方案;
(3)根据(2)问所得的方案,由一次函数的性质,结合x的取值范围即可得到合理建议.
(1)若派往A地区的乙型收割机为x台,则派往A地区的甲型收割机为(30-x)台;派往B地区的乙型收割机为(30-x)台,派往B地区的甲型收割机为(x-10)台,
∴y=1600x+1800(30-x)+1200(30-x)+1600(x-10)=200x+74000,
其中,x的取值范围是:10≤x≤30(x是正整数).
(2)由题意,令200x+74000≥79600,
解不等式,得x≥28 ,
由于10≤x≤30,
∴x取28,29,30这三个值,
∴有3种不同分配方案.
当x=28时,即派往A地区甲型收割机2台,乙型收割机28台;派往B 地区甲型收割机18台,乙型收割机2台;
当x=29时,即派往A地区甲型收割机1台,乙型收割机29台;派往B 地区甲型收割机19台,乙型收割机1台;
当x=30时,即30台乙型收割机全部派往A地区;20台甲型收割机全部派往B地区.
(3)由于一次函数y=200x+74000的值y是随着x的增大而增大的,所以,当x=30时,y取得最大值.
所以农机租赁公司将30台乙型收割机全部派往A地区;20台甲型收割要全部派往B地区,可使公司获得的租金最高.


科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。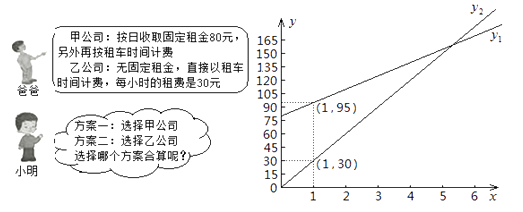
根据以上信息,解答下列问题:
(1)设租车时间为 ![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为 ![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 ![]() 元,分别求出
元,分别求出 ![]() ,
, ![]() 关于
关于 ![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=-x+m分别交于x轴、y轴于A,B两点,已知点C(2,0).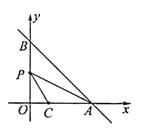
(1)当直线AB经过点C时,点O到直线AB的距离是;
(2)设点P为线段OB的中点,连结PA,PC,若∠CPA=∠ABO,则m的值是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某活动中心准备带会员去龙潭大峡谷一日游,1张儿童票和2张成人票共需190元,2张儿童票和3张成人票共需300元.解答下列问题:
(1)求每张儿童票和每张成人票各多少元?
(2)这个活动中心想带50人去游玩,费用不超过3000元,并且出于安全考虑,儿童人数不能超过22人,请你帮助活动中心确立出游方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一多边形草坪,在市政建设设计图纸上的面积为300cm2,其中一条边的长度为5cm.经测量,这条边的实际长度为15m,则这块草坪的实际面积是( )
A. 100m2 B. 270m2 C. 2700m2 D. 90000m2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)(x+2)(x﹣3)﹣x(x﹣4),其中x=﹣ ![]()
(2)(a+b)(a﹣b)+(a+b)2﹣2a2 , 其中a=3,b=﹣ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减/吨 | ﹣1 | +3 | ﹣2 | +4 | +7 | ﹣5 | ﹣10 |
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com