
����Ŀ����ͼ��ʾ��ij���̶�����ɽ�£�ɽ����Ϊֱ��l������һ��·����Ҫ����ɽ�µ��¶ȣ���tan����ֵ������Ա��ɽ��P�������ƴ������ߣ��۲����ɽ���ϵ�һ���������������C������Ϊ31�㣬����B������Ϊ26.6�㣮��֪����BC=40�ף������ڵ�ɽ��OB=240�ף�OA=300�ף�ͼ�еĵ�O��B��C��A��P��ͬһƽ���ڣ�
��
��1��P��OC�ľ��룮
��2��ɽ�µ��¶�tan����
�������sin26.6���0.45��tan26.6���0.50��sin31���0.52��tan37���0.60��
���𰸡�
��1��
�⣺��ͼ������P��PD��OC��D��PE��OA��E�����ı���ODPEΪ���Σ�
��Rt��PBD�У��ߡ�BDP=90�㣬��BPD=26.6�㣬
��BD=PDtan��BPD=PDtan26.6�㣻
��Rt��CPD�У��ߡ�CDP=90�㣬��CPD=31�㣬
��CD=PDtan��CPD=PDtan31�㣻
��CD��BD=BC��
��PDtan31�㩁PDtan26.6��=40��
��0.60PD��0.50PD=40��
���PD=400���ף���
��P��OC�ľ���Ϊ400��
��2��
�⣺��Rt��PBD�У�BD=PDtan26.6���400��0.50=200���ף���
��OB=240�ף�
��PE=OD=OB��BD=40�ף�
��OE=PD=400�ף�
��AE=OE��OA=400��300=100���ף���
��tan��= ![]() =0.4��
=0.4��
���¶�Ϊ0.4��
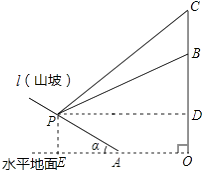
����������1������P��PD��OC��D��PE��OA��E�����ı���ODPEΪ���Σ��Ƚ�Rt��PBD���ó�BD=PDtan26.6�㣻��Rt��CPD���ó�CD=PDtan31�㣻�ٸ���CD��BD=BC���г����̣����PD=400������õ�P��OC�ľ��룻��2��������õ��߶�PD�ij����PE=40��AE=100��Ȼ���ڡ�APE���������Ǻ����Ķ��弴����⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
��1�����㣺 ![]() +cos245�㩁����2����1��|��
+cos245�㩁����2����1��|�� ![]() |
|
��2���Ȼ�������ֵ���� ![]() ��
�� ![]() ����
���� ![]() ������x=2
������x=2 ![]() ��y=
��y= ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��O�У��뾶OD����AB�ڵ�C������AO���ӳ�����O�ڵ�E������EC����AB=8��CD=2����EC�ij���Ϊ�� �� 
A.2 ![]()
B.8
C.2 ![]()
D.2 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��С�����������A������۲��ٹ�������ǽ���ϵĵ�����Ļ�������Ļ�϶�C��������Ϊ30�㣬���������Ե�����Ļ����ǰ��7m����B�����ֲ�ø���Ļ�϶�C��������Ϊ45�㣮��֪������Ļ���¶��뿪�������DEΪ4m��С����۾������1.60m��������Ļ���϶���ǽ��Ķ���ƽ�룮�������Ļ�϶����¶�֮��ľ���CD������������ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������OABC����ƽ��ֱ������ϵ�У�O��ԭ�㣬A������Ϊ��1�� ![]() �������C������Ϊ�� ��
�������C�������� �� 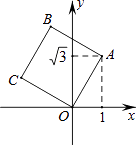
A.���� ![]() ��1��
��1��
B.����1�� ![]() ��
��
C.�� ![]() ��1��
��1��
D.���� ![]() ����1��
����1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���B=��C=36�㣬AB�Ĵ�ֱƽ���߽�BC�ڵ�D����AB�ڵ�H��AC�Ĵ�ֱƽ���߽�BC�ڵ�E����AC�ڵ�G������AD��AE�������н��۴�����ǣ� �� 
A.![]() =
= ![]()
B.AD��AE����BAC���ȷ�
C.��ABE�ա�ACD
D.S��ADH=S��CEG
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������y= ![]() ��ͼ����һ�κ���y=kx+b��ͼ����A��B���㣬��A������Ϊ��2��6������B������Ϊ��n��1����
��ͼ����һ�κ���y=kx+b��ͼ����A��B���㣬��A������Ϊ��2��6������B������Ϊ��n��1���� 
��1������������һ�κ����ı���ʽ��
��2����EΪy����һ�����㣬��S��AEB=10�����E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����D��BC���е㣬BF��AC�ڵ�F����AD�ڵ�E����BAC=45�㣮��֤����AEF�ա�BCF�� 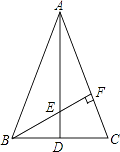
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�E��FΪ�Խ���AC�ϵ����㣬��AE=CF������DE��BF.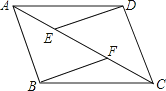
��1��д��ͼ�����е�ȫ�������Σ�
��2����֤��DE��BF��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com