
【题目】如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( ) 
A.![]() =
= ![]()
B.AD,AE将∠BAC三等分
C.△ABE≌△ACD
D.S△ADH=S△CEG
【答案】A
【解析】解:∵∠B=∠C=36°, ∴AB=AC,∠BAC=108°,
∵DH垂直平分AB,EG垂直平分AC,
∴DB=DA,EA=EC,
∴∠B=∠DAB=∠C=∠CAE=36°,
∴△BDA∽△BAC,
∴ ![]() ,
,
又∵∠ADC=∠B+∠BAD=72°,∠DAC=∠BAC﹣∠BAD=72°,
∴∠ADC=∠DAC,
∴CD=CA=BA,
∴BD=BC﹣CD=BC﹣AB,
则 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,故A错误;
,故A错误;
∵∠BAC=108°,∠B=∠DAB=∠C=∠CAE=36°,
∴∠DAE=∠BAC﹣∠DAB﹣∠CAE=36°,
即∠DAB=∠DAE=∠CAE=36°,
∴AD,AE将∠BAC三等分,故B正确;
∵∠BAE=∠BAD+∠DAE=72°,∠CAD=∠CAE+∠DAE=72°,
∴∠BAE=∠CAD,
在△BAE和△CAD中,
∵ 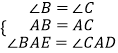 ,
,
∴△BAE≌△CAD,故C正确;
由△BAE≌△CAD可得S△BAE=S△CAD , 即S△BAD+S△ADE=S△CAE+S△ADE ,
∴S△BAD=S△CAE ,
又∵DH垂直平分AB,EG垂直平分AC,
∴S△ADH= ![]() S△ABD , S△CEG=
S△ABD , S△CEG= ![]() S△CAE ,
S△CAE ,
∴S△ADH=S△CEG , 故D正确.
故选:A.
由题意知AB=AC、∠BAC=108°,根据中垂线性质得∠B=∠DAB=∠C=∠CAE=36°,从而知△BDA∽△BAC,得 ![]() ,由∠ADC=∠DAC=72°得CD=CA=BA,进而根据黄金分割定义知
,由∠ADC=∠DAC=72°得CD=CA=BA,进而根据黄金分割定义知 ![]() =
= ![]() ,可判断A;根据∠DAB=∠CAE=36°知∠DAE=36°可判断B;根据∠BAD+∠DAE=∠CAE+∠DAE=72°可得∠BAE=∠CAD,可证△BAE≌△CAD,即可判断C;由△BAE≌△CAD知S△BAD=S△CAE , 根据DH垂直平分AB,EG垂直平分AC可得S△ADH=S△CEG , 可判断D.
,可判断A;根据∠DAB=∠CAE=36°知∠DAE=36°可判断B;根据∠BAD+∠DAE=∠CAE+∠DAE=72°可得∠BAE=∠CAD,可证△BAE≌△CAD,即可判断C;由△BAE≌△CAD知S△BAD=S△CAE , 根据DH垂直平分AB,EG垂直平分AC可得S△ADH=S△CEG , 可判断D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线y= ![]() x+1与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
x+1与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
(1)求抛物线的解析式;
(2)证明:圆C与x轴相切;
(3)过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F,求BE:MF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑物BC上有一旗杆AB,从与BC相距38m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆的高度约为 m.(结果精确到0.1m,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为31°,塔底B的仰角为26.6°.已知塔高BC=40米,塔所在的山高OB=240米,OA=300米,图中的点O、B、C、A、P在同一平面内.
求:
(1)P到OC的距离.
(2)山坡的坡度tanα.
(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin31°≈0.52,tan37°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= ![]() ,tan
,tan ![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系. 
(1)求点P的坐标;
(2)水面上升1m,水面宽多少( ![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为14.4km(即MC=14.4km).在A点测得岛屿的西端点M在点A的北偏东42°方向;航行4km后到达B点,测得岛屿的东端点N在点B的北偏东56°方向,(其中N,M,C在同一条直线上),求钓鱼岛东西两端点MN之间的距离(结果精确到0.1km).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,sin56°≈0.83,cos56°≈0.56,tan56°≈1.48)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AO是角平分线,D为AO上一点,作△CDE,使DE=DC,∠EDC=∠BAC,连接BE.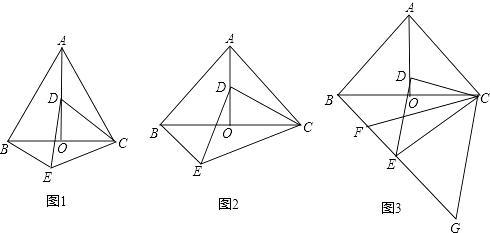
(1)若∠BAC=60°,求证:△ACD≌△BCE;
(2)若∠BAC=90°,AD=DO,求 ![]() 的值;
的值;
(3)若∠BAC=90°,F为BE中点,G为 BE延长线上一点,CF=CG,AD=nDO,直接写出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批同型号的彩电,第一个月售出50台,为了减少库存,第二个月每台降价500元将这批彩电全部售出,两个月的销售量的比是9:10,已知第一个月的销售额与第二个月的销售额相等,这两个月销售总额超过40万元.
(1)求第一个月每台彩电销售价格;
(2)这批彩电最少有多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com