
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与X轴交于点A、B两点B处的坐标为(3,0),与y轴交于c(0,﹣3),点P是直线BC下方抛物线上的动点.
(1)求出二次函数的解析式;
(2)连接PO、PC,并将△POC沿y轴对折,得到四边形POP′C,那么是否存在点P,使得四边形POP′C为菱形?若存在,求出点P的坐标,若存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P的坐标和四边形ABPC的最大面积.
【答案】
(1)解:把B(3,0)、C(0,﹣3)代入y=x2+bx+c,得
![]() ,解得
,解得 ![]() ,
,
∴这个二次函数的表达式为y=x2﹣2x﹣3
(2)解:存在.理由如下:
如图1中,作OC的垂直平分线交直线BC下方的抛物线于点P,垂足为点E.

则PO=PC,
∵△POC沿CO翻折,得到四边形POP′C,
∴OP′=OP,CP′=CP,
∴OP′=OP=CP′=CP,
∴四边形POP′C为菱形,
∵C点坐标为(0,﹣3),
∴E点坐标为(0,﹣ ![]() ),
),
∴点P的纵坐标为﹣ ![]() ,
,
把y=﹣ ![]() 代入y=x2﹣2x﹣3得x2﹣2x﹣3=﹣
代入y=x2﹣2x﹣3得x2﹣2x﹣3=﹣ ![]() ,
,
解得x= ![]() ,
,
∵点P在直线BC下方的抛物线上,
∴x= ![]() ,
,
∴满足条件的点P的坐标为( ![]() ,﹣
,﹣ ![]() ).
).
(3)解:如图2中,作PF⊥x轴于F点,交BC于E点,BC的解析式为y=x﹣3,设E(m,m﹣3),P(m,m2﹣2m﹣3).
 ,
,
PE=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m=﹣(m﹣ ![]() )2+
)2+ ![]() ,
,
S△BCP=S△BEP+SCEP= ![]() PE×FB+
PE×FB+ ![]() EPOF
EPOF
= ![]() EPOB
EPOB
= ![]() ×3[﹣(m﹣
×3[﹣(m﹣ ![]() )2+
)2+ ![]() ]
]
=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() ,
,
∵﹣ ![]() <0,
<0,
∴当m= ![]() 时,S最大=
时,S最大= ![]() ,
,
此时P( ![]() ,﹣
,﹣ ![]() );
);
∵A(﹣1,0),B(3,0),C(0,﹣3),
∵四边形ACPB的面积=△ABC的面积+△PBC的面积,△ABC的面积= ![]() ×4×3=6=定值,
×4×3=6=定值,
∴当△PBC的面积最大时,四边形ACPB的面积最大,最大值为6+ ![]() =
= ![]()
【解析】1)将点B、C代入y=x2+bx+c可得到关于b、c的方程组,解方程组求即可。
(2)作OC的垂直平分线交直线BC下方的抛物线于点P,则PO=PC,根据翻折的性质得OP′=OP,CP′=CP,易证得四边形POP′C为菱形,就可以求得点E的坐标,将点P的纵坐标代入二次函数解析式,可求出对应x的值,根据点P在直线BC下方的抛物线上,然后确定满足条件的P点坐标。
(3)添加辅助线,作PF⊥x轴于F点,交BC于E点,BC的解析式为y=x-3,设E(m,m-3),P′(m,m2-2m-3).根据S△BCP=S△BEP+SCEP,构建s与m的二次函数,求出二次函数的顶点坐标,求出△PBC的面积的最大值,即可解决问题。
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握二次函数的最值(如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a)的相关知识才是答题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,要设计一个等腰梯形的花坛,花坛上底120米,下底180米,上下底相距80米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为x米.
(1)用含x的式子表示横向甬道的面积;
(2)当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
(3)根据设计的要求,甬道的宽不能超过6米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是5.7,花坛其余部分的绿化费用为每平方米0.02万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A,B,C三点坐标分别为A(﹣6,3),B(﹣4,1),C(﹣1,1).
(1)如图1,顺次连接AB,BC,CA,得△ABC.
①点A关于x轴的对称点A1的坐标是 , 点B关于y轴的对称点B1的坐标是;
②画出△ABC关于原点对称的△A2B2C2;
③tan∠A2C2B2=;
(2)利用四边形的不稳定性,将第二象限部分由小正方形组成的网格,变化为如图2所示的由小菱形组成的网格,每个小菱形的边长仍为1个单位长度,且较小内角为60°,原来的格点A,B,C分别对应新网格中的格点A′,B′,C′,顺次连接A′B′,B′C′,C′A′,得△A′B′C′,则tan∠A′C′B′= . 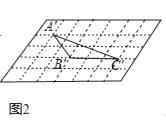
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场对某种商品进行销售,第x天的销售单价为m元/件,日销售量为n件,其中m,n分别是x(1≤x≤30,且x为整数)的一次函数,销售情况如表:
销售第x天 | 第1天 | 第2天 | 第3天 | 第4天 | … | 第30天 |
销售单价m(元/件) | 49 | 48 | 47 | 46 | … | 20 |
日销售量n(件) | 45 | 50 | 55 | 60 | … | 190 |
(1)观察表中数据,分别直接写出m与x,n与x的函数关系式: , ;
(2)求商场销售该商品第几天时该商品的日销售额恰好为3600元?
(3)销售商品的第15天为儿童节,请问:在儿童节前(不包括儿童节当天)销售该商品第几天时该商品的日销售额最多?商场决定将这天该商品的日销售额捐献给儿童福利院,试求出商场可捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂生产上第世博会吉祥物:“海宝”纪念章10万个,质检部门为检测这批纪念章质量的合格情况,从中随机抽查500个,合格499个![]() 下列说法正确的是
下列说法正确的是![]()
![]()
A. 总体是10万个纪念章的合格情况,样本是500个纪念章的合格情况
B. 总体是10万个纪念章的合格情况,样本是499个纪念章的合格情况
C. 总体是500个纪念章的合格情况,样本是500个纪念章的合格情况
D. 总体是10万个纪念章的合格情况,样本是1个纪念章的合格情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个足球的质量以400克为标准,用正数记超过标准质量的克数,用负数记不足标准质量的克数![]() 下面是5个足球的质量检测结果
下面是5个足球的质量检测结果![]() 单位:克
单位:克![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 写出这5个足球的质量;
写出这5个足球的质量;
![]() 请指出选用哪一个足球好些,并用绝对值的知识进行说明.
请指出选用哪一个足球好些,并用绝对值的知识进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保护学生的身体健康,某中学课桌椅的高度都是按一定的关系(一次函数)配套设计的,下表列出5套符合条件的课桌椅的高度. ①假设课桌的高度为ycm椅子的高度为xcm,请确定y与x的函数关系式;②现有一把高37cm的椅子和一张高71.5cm的课桌,它们是否配套?为什么?
椅子高度x(cm) | 45 | 42 | 39 | 36 | 33 |
桌子高度y(cm) | 84 | 79 | 74 | 69 | 64 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,点P的坐标为(m+1,m﹣1).
(1)试判断点P是否在一次函数y=x﹣2的图象上,并说明理由;
(2)如图,一次函数y=﹣ ![]() x+3的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围.
x+3的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围.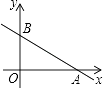
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com