
����Ŀ��ij�̳���ij����Ʒ�������ۣ���x������۵���ΪmԪ/������������Ϊn��������m��n�ֱ���x��1��x��30����xΪ��������һ�κ�����������������
���۵�x�� | ��1�� | ��2�� | ��3�� | ��4�� | �� | ��30�� |
���۵���m��Ԫ/���� | 49 | 48 | 47 | 46 | �� | 20 |
��������n������ | 45 | 50 | 55 | 60 | �� | 190 |
��1���۲�������ݣ��ֱ�ֱ��д��m��x��n��x�ĺ�����ϵʽ�� �� ��
��2�����̳����۸���Ʒ�ڼ���ʱ����Ʒ�������۶�ǡ��Ϊ3600Ԫ��
��3��������Ʒ�ĵ�15��Ϊ��ͯ�ڣ����ʣ��ڶ�ͯ��ǰ����������ͯ�ڵ��죩���۸���Ʒ�ڼ���ʱ����Ʒ�������۶���ࣿ�̳��������������Ʒ�������۶������ͯ����Ժ��������̳��ɾ�����Ԫ��
���𰸡�
��1��m=��x+50,n=5x+40
��2���⣺��������ã�����x+50����5x+40��=3600��
�����ã�x2��42x+320=0��
��ã�x1=10��x2=32��
��32��30��
��x=32��ȥ��
�𣺵�10��������۶�Ϊ3600Ԫ
��3���⣺�������۶�ΪwԪ��
��������ã�w=����x+50����5x+40��=��5x2+210x+2000=��5��x��21��2+4205��
��a=��5��0��
�������߿������£�
�֡߶Գ���Ϊֱ��x=21��
�൱1��x��14ʱ��w��x�����������
�൱x=14ʱ��wȡ���ֵ�����ֵΪ3960��
���ڶ�ͯ��ǰ����������ͯ�ڵ��죩���۸���Ʒ��14��ʱ����Ʒ�������۶���࣬�̳��ɾ��3960Ԫ��
����������1���۲�������ݿ�֪��ÿ��һ�죬���۵��۽���1Ԫ/������������5����
��m=49����x��1��=��x+50��n=45+5��x��1��=5x+40��
���Դ��ǣ�m=��x+50��n=5x+40��
��2������������=����![]() ���������ת��Ϊ���̣���x+50����5x+40��=3600����3����ֵ�����蹹�������������۶�Ϊw=����x+50����5x+40��=��5x2+210x+2000=��5��x��21��2+4205��������ֵ����.
���������ת��Ϊ���̣���x+50����5x+40��=3600����3����ֵ�����蹹�������������۶�Ϊw=����x+50����5x+40��=��5x2+210x+2000=��5��x��21��2+4205��������ֵ����.


 ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCDΪƽ���ı������ӳ�AD��E��ʹDE=AD������EB��EC��DB������һ������������ʹ�ı���DBCE��Ϊ���ε����� ��

��A��AB=BE ��B��BE��DC ��C����ADB=90�� ��D��CE��DE
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ֱ��MN����O��A��B���㣬AC��ֱ����ADƽ�֡�CAM����O��D����D��DE��MN��E��
��1����֤��DE�ǡ�O�����ߣ�
��2����DE=6cm��AE=3cm�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����һ�����ǰ��е�����ֱ�����dzߵ�ֱ�Ƕ���C����ͼ��ʾ�ķ�ʽ������һ�𣬵���ACE��180���ҵ�E��ֱ��AC���Ϸ�ʱ������������ACE��_____�������ǰ�BCE��һ������б��ADƽ�У���д�����п��������
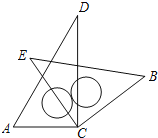
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����D��E�ֱ�����ABC�ı�AB��AC���е㣮
(1)��ͼ1����O����ABC�ڵĶ��㣬��O��F�ֱ���OB��OC���е㣬��֤��DEFG��ƽ���ı��Σ�
(2)��ͼ2����BE��DC�ڵ�O������AO���ӳ��߾���BC���е���Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y=x2+bx+c��ͼ����X�ύ�ڵ�A��B����B��������Ϊ��3��0������y�ύ��c��0����3������P��ֱ��BC�·��������ϵĶ��㣮
��1��������κ����Ľ���ʽ��
��2������PO��PC��������POC��y����ۣ��õ��ı���POP��C����ô�Ƿ���ڵ�P��ʹ���ı���POP��CΪ���Σ������ڣ������P�����꣬�����ڣ���˵�����ɣ�
��3������P�˶���ʲôλ��ʱ���ı���ABPC�������������ʱP��������ı���ABPC����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ� С����ѧϰ���θ�ʽ����һЩ�����ŵ�ʽ�ӿ���д����һ��ʽ�ӵ�ƽ�����磺![]() ������˼����С������������̽����
������˼����С������������̽����
��![]() ������
������![]() ��������������
��������������![]() ��
��
��![]() ������С�����ҵ���һ�ְѲ���
������С�����ҵ���һ�ְѲ���![]() ��ʽ�ӻ�Ϊƽ��ʽ�ķ�����
��ʽ�ӻ�Ϊƽ��ʽ�ķ�����
�������С���ķ���̽��������������⣺
��![]() ��Ϊ������ʱ����
��Ϊ������ʱ����![]() ���ú�m��n��ʽ�ӷֱ��ʾ
���ú�m��n��ʽ�ӷֱ��ʾ![]() ����
����![]() ���� ����
���� ����![]() ���� ����
���� ����
��2��������̽���Ľ��ۣ���һ��������![]() ����գ� ���� ����(�� ������ ��
����գ� ���� ����(�� ������ ��![]() )2��
)2��
��3����![]() ����
����![]() ������������
��Ϊ����������![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC����AB=AC��D��BC���е�����ACΪ������������ֱ����ACE����EAC=90�㣬����BE����AD�ڵ�F����AC�ڵ�G.
(1)����BAC=40�㣬���AEB�Ķ�����
(2)��֤:��AEB=��ACF.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���� ![]() ���߳�Ϊ1��������ƴ�ӳ�һ�ţ����
���߳�Ϊ1��������ƴ�ӳ�һ�ţ���� ![]() ��
�� ![]() ��
�� ![]() ������
������ ![]() �� �������˹��ɣ�д��
�� �������˹��ɣ�д�� ![]() ���ú�
���ú� ![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com