
【题目】在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
(1)若∠BAC=40°,求∠AEB的度数;
(2)求证:∠AEB=∠ACF.

【答案】(1)25°;(2)证明见解析.
【解析】
(1)已知AB=AC,△ACE是等腰直角三角形,可得AB=AE;再由等腰三角形的性质可得∠ABE=∠AEB,由已知条件求出∠BAE的度数,再根据三角形内角和定理即可求出∠AEB的度数;(2)根据等腰三角形的性质得出∠BAF=∠CAF,根据SAS推出△BAF≌△CAF,根据全等得出∠ABF=∠ACF,即可证得结论.
(1) ∵AB=AC,△ACE是等腰直角三角形,
∴AB=AE,
∴∠ABE=∠AEB,
又∵∠BAC=40°,∠EAC=90°,
∴∠BAE=40°+90°=130°,
∴∠AEB=(180°-130°)÷2=25°.
(2)证明:∵AB=AC,D是BC的中点,
∴∠BAF=∠CAF.
在△BAF和△CAF中
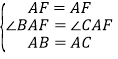
∴△BAF≌△CAF(SAS),
∴∠ABF=∠ACF,
∵∠ABE=∠AEB,
∴∠AEB=∠ACF.


科目:初中数学 来源: 题型:
【题目】某校学生会主席换届选举,经初选、复选后,共有甲,乙,丙三人进入最后的竞选,最后决定用投票方式进行选举,共发出1800张选票,得票数最高者为当选人,且废票不计入任何一位候选人的得票数内,全校设有四个投票箱,目前第一、第二、第三投票箱已开完所有选票,剩下第四投票箱尚未开票,结果如表所示:![]() 单位:票
单位:票![]()
投票箱 | 候选人 | 废票 | 合计 | ||
甲 | 乙 | 丙 | |||
一 | 200 | 211 | 147 | 12 | 570 |
二 | 244 | 15 | 630 | ||
三 | 97 | 41 | 205 | 7 | 350 |
四 | 250 | ||||
![]() 若第二投票箱候选人甲的得票数比乙的3倍还多31票,请分别求出第二投票箱甲、乙两名候选人的得票数.
若第二投票箱候选人甲的得票数比乙的3倍还多31票,请分别求出第二投票箱甲、乙两名候选人的得票数.
![]() 根据
根据![]() 题的数据分析,请判断乙侯选人是否还有机会当选,并详细解释或完整写出你的解题过程.
题的数据分析,请判断乙侯选人是否还有机会当选,并详细解释或完整写出你的解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场对某种商品进行销售,第x天的销售单价为m元/件,日销售量为n件,其中m,n分别是x(1≤x≤30,且x为整数)的一次函数,销售情况如表:
销售第x天 | 第1天 | 第2天 | 第3天 | 第4天 | … | 第30天 |
销售单价m(元/件) | 49 | 48 | 47 | 46 | … | 20 |
日销售量n(件) | 45 | 50 | 55 | 60 | … | 190 |
(1)观察表中数据,分别直接写出m与x,n与x的函数关系式: , ;
(2)求商场销售该商品第几天时该商品的日销售额恰好为3600元?
(3)销售商品的第15天为儿童节,请问:在儿童节前(不包括儿童节当天)销售该商品第几天时该商品的日销售额最多?商场决定将这天该商品的日销售额捐献给儿童福利院,试求出商场可捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个足球的质量以400克为标准,用正数记超过标准质量的克数,用负数记不足标准质量的克数![]() 下面是5个足球的质量检测结果
下面是5个足球的质量检测结果![]() 单位:克
单位:克![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 写出这5个足球的质量;
写出这5个足球的质量;
![]() 请指出选用哪一个足球好些,并用绝对值的知识进行说明.
请指出选用哪一个足球好些,并用绝对值的知识进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,将△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.
(1)画出△A1B1C1和△A2B2C2;
(2)△ABC经旋转、平移后点A的对应点分别为A1、A2,请写出点A1、A2的坐标;
(3)P(a,b)是△ABC的边AC上一点,△ABC经旋转、平移后点P的对应点分别为P1,P2,请写出点P1、P2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保护学生的身体健康,某中学课桌椅的高度都是按一定的关系(一次函数)配套设计的,下表列出5套符合条件的课桌椅的高度. ①假设课桌的高度为ycm椅子的高度为xcm,请确定y与x的函数关系式;②现有一把高37cm的椅子和一张高71.5cm的课桌,它们是否配套?为什么?
椅子高度x(cm) | 45 | 42 | 39 | 36 | 33 |
桌子高度y(cm) | 84 | 79 | 74 | 69 | 64 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点A(0,6)的直线AB与直线OC相交于点C(2,4)动点P沿路线O→C→B运动.(1)求直线AB的解析式;(2)当△OPB的面积是△OBC的面积的![]() 时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.
时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图点A(1,1),B(2,﹣3),点P为x轴上一点,当|PA﹣PB|最大时,点P的坐标为( )

A. (﹣1,0) B. (![]() ,0) C. (
,0) C. (![]() ,0) D. (1,0)
,0) D. (1,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
如图①,图形l外一点P与图形l上各点连接的所有线段中,若线段PA1最短,则线段PA1的长度称为点P到图形l的距离.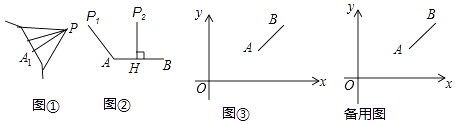
例如:图②中,线段P1A的长度是点P1到线段AB的距离;线段P2H的长度是点P2到线段AB的距离.
解决问题:
如图③,平面直角坐标系xOy中,点A、B的坐标分别为(8,4),(12,7),点P从原点O出发,以每秒1个单位长度的速度向x轴正方向运动了t秒.
(1)当t=4时,求点P到线段AB的距离;
(2)t为何值时,点P到线段AB的距离为5?
(3)t满足什么条件时,点P到线段AB的距离不超过6?(直接写出此小题的结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com