
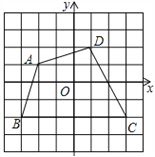
【题目】 如图,已知四边形ABCD(网格中每个小正方形的边长均为1).
(1)写出点A,B,C,D的坐标;
(2)求四边形ABCD的面积.
科目:初中数学 来源: 题型:
【题目】某工厂生产的某种产品按质量分为1 0个档次.第1档次(最低档次)的产品一天能生产7 6件,每件利润10元.每提高一个档次,每件利润增加2元,但一天产量减少4件.若生产第x档次的产品一天的总利润为1080元,求该产品的质量档次。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB∥CD,EF分别交AB、CD于点M、N,NP平分∠MND. 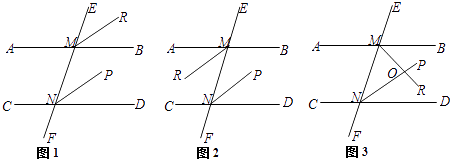
(1)如图1,若MR平分∠EMB,则MR∥NP.请你把下面的解答过程补充完整: 解:因为AB∥CD(已知)
所以∠EMB=∠END()
因为MR平分∠EMB,NP平分∠MND(已知)
所以∠EMR= ![]() ∠EMB,∠MNP=
∠EMB,∠MNP= ![]() ∠MND(角平分线定义)
∠MND(角平分线定义)
所以∠EMR=∠MNP
所以MR∥NP()
(2)如图2,若MR平分∠AMN,则MR与NP又怎样的位置关系?请在横线上写出你的猜想结论:;
(3)如图3,若MR平分∠BMN,则MR与NP又怎样的位置关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
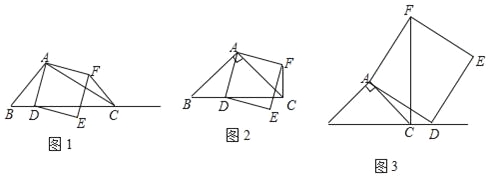
【题目】如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,联结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,将△ABD绕A点逆时针旋转90°,所得到的三角形为 ,线段CF、BD所在直线的位置关系为 ,线段CF、BD的数量关系为 ;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)在给定方格纸中画出平移后的△A′B′C′;画出AB边上的中线CD;画出BC边上的高线AE;
(2)△A′B′C′的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标是( )
A.(﹣4,0)
B.(6,0)
C.(﹣4,0)或(6,0)
D.(0,12)或(0,﹣8)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com