
【题目】直线AB∥CD,EF分别交AB、CD于点M、N,NP平分∠MND. 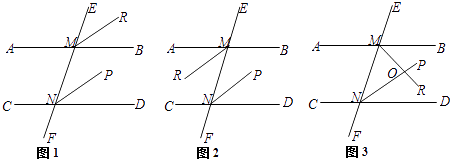
(1)如图1,若MR平分∠EMB,则MR∥NP.请你把下面的解答过程补充完整: 解:因为AB∥CD(已知)
所以∠EMB=∠END()
因为MR平分∠EMB,NP平分∠MND(已知)
所以∠EMR= ![]() ∠EMB,∠MNP=
∠EMB,∠MNP= ![]() ∠MND(角平分线定义)
∠MND(角平分线定义)
所以∠EMR=∠MNP
所以MR∥NP()
(2)如图2,若MR平分∠AMN,则MR与NP又怎样的位置关系?请在横线上写出你的猜想结论:;
(3)如图3,若MR平分∠BMN,则MR与NP又怎样的位置关系?请说明理由.
【答案】
(1)两直线平行,同位角相等;同位角相等,两直线平行
(2)MR∥NP
(3)解:MR⊥NP;理由如下:
因为AB∥CD,
所以∠BMN+∠MND=180°,
因为MR平分∠BMN,NP平分∠MND,
所以∠RMN= ![]() ∠BMN,∠MNP=
∠BMN,∠MNP= ![]() ∠MND,
∠MND,
所以∠RMN+∠MNP= ![]() (∠BMN+∠MND)=90°,
(∠BMN+∠MND)=90°,
所以∠MON=90°,
所以MR⊥NP
【解析】解:(1)因为AB∥CD(已知)所以∠EMB=∠END(两直线平行,同位角相等)因为MR平分∠EMB,NP平分∠MND(已知)所以∠EMR= ![]() ∠EMB,∠MNP=
∠EMB,∠MNP= ![]() ∠MND(角平分线定义)所以∠EMR=∠MNP所以MR∥NP(同位角相等,两直线平行)所以答案是:两直线平行,同位角相等;同位角相等,两直线平行; (2)MR∥NP;理由如下:因为AB∥CD(已知)所以∠AMN=∠MND(两直线平行,内错角相等)因为MR平分∠AMN,NP平分∠MND(已知)所以∠NMR=
∠MND(角平分线定义)所以∠EMR=∠MNP所以MR∥NP(同位角相等,两直线平行)所以答案是:两直线平行,同位角相等;同位角相等,两直线平行; (2)MR∥NP;理由如下:因为AB∥CD(已知)所以∠AMN=∠MND(两直线平行,内错角相等)因为MR平分∠AMN,NP平分∠MND(已知)所以∠NMR= ![]() ∠AMN,∠MNP=
∠AMN,∠MNP= ![]() ∠MND(角平分线定义)所以∠NMR=∠MNP所以MR∥NP(内错角相等,两直线平行)所以答案是:MR∥NP;
∠MND(角平分线定义)所以∠NMR=∠MNP所以MR∥NP(内错角相等,两直线平行)所以答案是:MR∥NP;
【考点精析】根据题目的已知条件,利用平行线的判定与性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


科目:初中数学 来源: 题型:
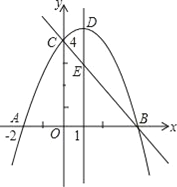
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,OC为∠AOB的角平分线, 
(1)作图: ①在OA边上任取一点P,过点P作PD∥OB,交OC于点D;
②过点D作DE⊥OB,垂足为点E.
(2)求∠PDE的度数.
(3)若∠PDO=40°,求∠AOB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题的是( )
A. 内错角相等 B. 等腰三角形一定是等边三角形
C. 两边以及一个角对应相等的两个三角形全等 D. 全等三角形的对应边相等
查看答案和解析>>
科目:初中数学 来源: 题型:
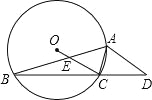
【题目】如图所示,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D点,OC交AB于E点.
(1)求∠D的度数;
(2)求证:AC2=ADCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(5,3),点C(0,8),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标;
(2)求△ABC的面积;
(3)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中,①∠A+∠B=∠C; ②∠A:∠B:∠C=1:2:3; ③∠A=![]() ∠B=
∠B=![]() ∠C;
∠C;
④∠A=∠B=2∠C; ⑤∠A=2∠B=3∠C,能确定△ABC为直角三角形的条件有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
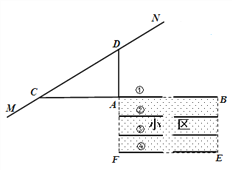
【题目】根据规定:距离高铁轨道 200米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.
如图是一个小区平面示意图,矩形ABEF为一新建小区,直线MN为高铁轨道,C、D是直线MN上的两点,点C、A、B在一直线上,且DA⊥CA,∠ACD=30°,AD=220.某人看中了①号楼A单元的一套住宅,但是感觉小区距离高铁轨道这么近,易受噪音污染,而售楼人员却说,虽然A单元离高铁轨道最近,但是AD长达220米,是达到设计要求的.
(1) 你认为售楼人员的话是否可信?为什么?
(2) 若一列长度为228米的高铁以70米/秒的速度通过时,则A单元用户受到影响时间有多长?(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7,
≈1.7, ![]() ≈61)
≈61)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com