
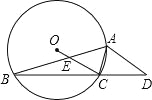
【题目】如图所示,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D点,OC交AB于E点.
(1)求∠D的度数;
(2)求证:AC2=ADCE.
【答案】(1)45°
(2)证明见解析
【解析】
试题分析: (1)连接OA,由圆周角∠ABC与圆心角∠AOC所对的弧为同一条弧,根据同弧所对的圆心角等于所对圆周角的2倍,由∠ABC的度数求出∠AOC的度数,再由OA=OC,根据等边对等角,由顶角∠AOC的度数,利用三角形的内角和定理求出底角∠ACO的度数,再由∠BAC及∠ABC的度数,求出∠ACB的度数,由∠ACB﹣∠ACO求出∠BCE的度数,由OC与AD平行,根据两直线平行同位角相等可得∠D=∠BCE,可得出∠D的度数;
(2)由∠ACB的度数,利用邻补角定义求出∠ACD的度数,再由∠AEC为三角形BEC的外角,利用外角性质得到∠AEC=∠ABC+∠BCE,可得出∠AEC的度数,进而得到∠AEC=∠ACD,在三角形ACD中,由∠ACD及∠D的度数,求出∠CAD的度数,可得∠CAD=∠ACE,利用两对对应角相等的三角形相似可得三角形AEC与三角形DCA相似,根据相似三角形的对应边成比例可得证.
解:(1)连接OA,如图所示:

∵圆周角∠ABC与圆心角∠AOC所对的弧都为![]() ,
,
∴∠AOC=2∠ABC,又∠ABC=15°,
∴∠AOC=30°,
又OA=OC,∴∠OAC=∠OCA=![]() =75°,
=75°,
又∠BAC=45°,∠ABC=15°,
∴∠ACB=120°,
∴∠OCB=∠ACB﹣∠ACO=120°﹣75°=45°,
又OC∥AD,
∴∠D=∠OCB=45°;
(2)∵∠ABC=15°,∠OCB=45°,
∴∠AEC=60°,
又∠ACB=120°∴∠ACD=60°,
∴∠AEC=∠ACD=60°,
∵∠D=45°,∠ACD=60°,
∴∠CAD=75°,又∠OCA=75°,
∴∠CAD=∠OCA=75°,
∴△ACE∽△DAC,
∴![]() =
=![]() ,即AC2=ADCE.
,即AC2=ADCE.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】直线AB∥CD,EF分别交AB、CD于点M、N,NP平分∠MND. 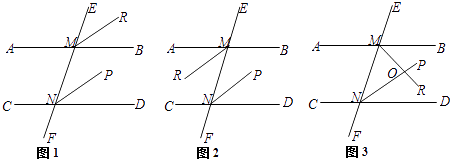
(1)如图1,若MR平分∠EMB,则MR∥NP.请你把下面的解答过程补充完整: 解:因为AB∥CD(已知)
所以∠EMB=∠END()
因为MR平分∠EMB,NP平分∠MND(已知)
所以∠EMR= ![]() ∠EMB,∠MNP=
∠EMB,∠MNP= ![]() ∠MND(角平分线定义)
∠MND(角平分线定义)
所以∠EMR=∠MNP
所以MR∥NP()
(2)如图2,若MR平分∠AMN,则MR与NP又怎样的位置关系?请在横线上写出你的猜想结论:;
(3)如图3,若MR平分∠BMN,则MR与NP又怎样的位置关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
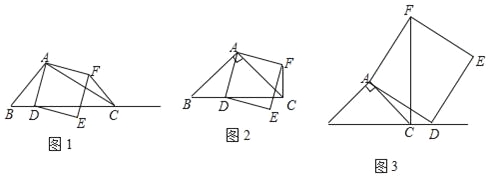
【题目】如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,联结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,将△ABD绕A点逆时针旋转90°,所得到的三角形为 ,线段CF、BD所在直线的位置关系为 ,线段CF、BD的数量关系为 ;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)在给定方格纸中画出平移后的△A′B′C′;画出AB边上的中线CD;画出BC边上的高线AE;
(2)△A′B′C′的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com