Question

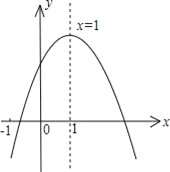
【题目】已知二次函数y=ax2+bx+c （a≠0）的图象如图所示，有下列5个结论：

①abc＜0；　②b＜a+c；　③4a+2b+c＞0；④2c＜3b；⑤a+b＜m （am+b）（m≠1的实数），其中结论正确的个数有（　　）

A. 2个 B. 3个 C. 4个 D. 5个

Answer 1

【答案】B

【解析】由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．

解：①图象开口向下，与y轴交于正半轴，对称轴为x=1，能得到：a＜0，c＞0， =1，

∴b=﹣2a＞0，

∴abc＜0，此结论正确；

②当x=﹣1时，由图象知y＜0，

把x=﹣1代入解析式得：a﹣b+c＜0，

∴b＞a+c，

∴②错误；

③图象开口向下，与y轴交于正半轴，对称轴为x=1，

能得到：a＜0，c＞0， =1，

所以b=﹣2a，

所以4a+2b+c=4a﹣4a+c＞0．

∴③正确；

④∵由①②知b=﹣2a且b＞a+c，

∴2c＜3b，④正确；

⑤∵x=1时，y=a+b+c（最大值），

x=m时，y=am2+bm+c，

∵m≠1的实数，

∴a+b+c＞am2+bm+c，

∴a+b＞m（am+b）．

∴⑤错误．

故选：B．

“点睛”此题主要考查图象与二次函数系数之间的关系，二次函数与方程之间的转换，根的判别式的熟练运用．会利用特殊值代入法求得特殊的式子，如：y=a+b+c，y=a-b+c，然后根据图象判断其值．