解:原不等式两边同乘以30,得:15(3x-1)-10(4x-2)≥6(6x-3)-39,
化简得:-31x≥-62,
解得:x≤2,(5分)
设y=2|x-1|+|x+4|,
(1)当x≤-4时,y=-2(x-1)-(x+4)=-3x-2
所以,y的最小值都为(-3)×(-4)-2=10,此时x=-4;(10分)
(2)当-4≤x≤1时,y=-2(x-1)-(x+4)=-3x-2
所以,y的最小值为5,此时x=1;(15分)
(3)当1≤x≤2时,y=2(x-1)+(x+4)=3x+2
所以,y的最小值为5,此时x=1.(20分)
综上所述,2|x-1|+|x+4|的最小值为5,在x=1时取得.(25分)
分析:首先解出不等式的解集,再根据所求代数式的绝对值确定x的取值范围,根据x的取值范围确定代数式的最小值即可.
点评:本题考查了解绝对值代数式最值及不等式的解法.解带绝对值代数式的最值是本题的一个难点.

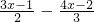
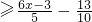 ,求2|x-1|+|x+4|的最小值
,求2|x-1|+|x+4|的最小值
