
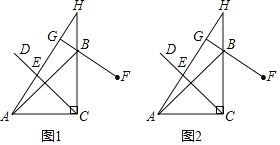
【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,E为∠ACB平分线CD上一动点(不与点C重合),点E关于直线BC的对称点为F,连接AE并延长交CB延长线于点H,连接FB并延长交直线AH于点G.
(1)求证:AE=BF.
(2)用等式表示线段FG,EG与CE的数量关系,并证明.
(3)连接GC,用等式表示线段GE,GC与GF的数量关系是 .
【答案】(1)详见解析;(2)结论:FG2+EG2=2EC2;(3)结论:GE+GF=![]() CG.
CG.
【解析】
(1)连结CF,证明△ACE≌△BCF(SAS)即可解决问题;
(2)结论:FG2+EG2=2EC2,连结EF,通过互补的角和四边形内角和证明∠EGF=90°,再由勾股定理即可解决问题;
(3)结论:GE+GF=![]() CG,证明Rt△CNE≌Rt△CMF(HL),Rt△GCN≌Rt△GCM(HL)即可解决问题.
CG,证明Rt△CNE≌Rt△CMF(HL),Rt△GCN≌Rt△GCM(HL)即可解决问题.
(1)证明:如图1中,连接CF,
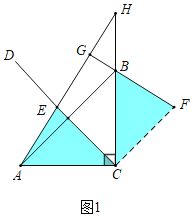
∵CD平分∠ACB,∠ACB=90°,
∴∠ACE=∠BCE=45°,
∵E,F关于CB对称,
∴∠BCF=∠BCE=45°,CE=CF,
∴∠ACE=∠BCF,
在△ACE和△BCF中,
 ,
,
∴△ACE≌△BCF(SAS),
∴AE=BF;
(2)解:结论:FG2+EG2=2EC2,
理由:连接EF,CF,
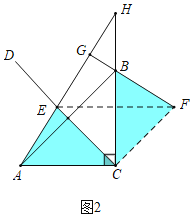
∵△ACE≌△BCF,
∴∠AEC=∠BFC,
∵∠AEC+∠CEG=180°,
∴∠CEG+∠CFG=180°,
∴∠ECF+∠EGF=180°,
∵∠ECB=∠BCF=45°,
∴∠ECF=∠EGF=90°,
∴FG2+EG2=EF2,EF2=CE2+CF2,
∵CE=CF,
∴FG2+EG2=2CE2,
(3)如图3中,结论:GE+GF=![]() CG,
CG,
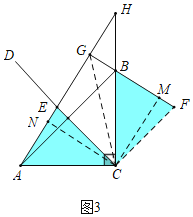
理由:连接CG,CF,作CM⊥BF于F,CN⊥AG于N,
∵△ACE≌△BCF,
∴CN=CM(全等三角形对应边上的高相等),
∵∠CNE=∠CMF=90°,CE=CF,
∴Rt△CNE≌Rt△CMF(HL),
∴EN=FM,
∵∠CNG=∠CMG=90°,CG=CG,
∴Rt△GCN≌Rt△GCM(HL),
∴GN=GM,∠CGN=∠CGM=45°,
∴CG=![]() GN,
GN,
∴GE+GF=GNEN+GM+MF=2GN=![]() CG.
CG.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),直线y=﹣![]() x+
x+![]() 与边AB,BC分别相交于点M,N,函数y=
与边AB,BC分别相交于点M,N,函数y=![]() (x>0)的图象过点M.
(x>0)的图象过点M.
(1)试说明点N也在函数y=![]() (x>0)的图象上;
(x>0)的图象上;
(2)将直线MN沿y轴的负方向平移得到直线M′N′,当直线M′N′与函数y═![]() (x>0)的图象仅有一个交点时,求直线M'N′的解析式.
(x>0)的图象仅有一个交点时,求直线M'N′的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,一架伸缩楼梯托架![]() 固定在墙面上,托架
固定在墙面上,托架![]() 始终与地面垂直且
始终与地面垂直且![]() .如图2, 旋转支撑臂
.如图2, 旋转支撑臂![]() 绕着点
绕着点![]() 旋转,当伸缩楼梯下放时,楼梯长
旋转,当伸缩楼梯下放时,楼梯长![]() 米,点
米,点![]() 正好接触地面,此时,旋转支撑臂
正好接触地面,此时,旋转支撑臂![]() 与楼梯托架
与楼梯托架![]() 之间的夹角为
之间的夹角为![]() ;当伸缩楼梯上收时,旋转支撑臂
;当伸缩楼梯上收时,旋转支撑臂![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() ,楼梯长
,楼梯长![]() 变为
变为![]() 米,此时,楼梯底部的脚垫
米,此时,楼梯底部的脚垫![]() 到地面的距离为( )米.
到地面的距离为( )米.

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位现要组织其市场和生产部的员工游览该公园,门票价格如下:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
如果按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1245元;如果两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为945元.那么该公司这两个部的人数之差的绝对值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
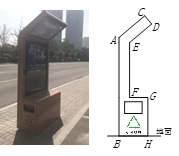
【题目】在太原迎泽西大街上有一种智能垃圾桶,这种智能垃圾桶不仅可以供行人休息,灯箱边的中部还有USB接口可供行人充电.此种垃圾桶的侧面示意图如图所示,其中AC∥ED,AB∥EF∥GH,CD=20cm,DE=60cm,EF=100m,GH=80cm,∠CDE=∠EFG=90°,∠DEF=130°,则此种垃圾桶的高度(C到地面的距离)约为________cm.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑤5a﹣2b<0;其中正确的个数有( )
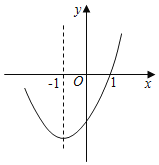
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图1,在△ABC看,把AB点绕点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形ABCD,∠C=90°,∠D=150°,BC=12,CD=2![]() ,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,给予证明,并求△PAB的“旋补中线”长;若不存在,说明理由.
,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,给予证明,并求△PAB的“旋补中线”长;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com