
【题目】在太原迎泽西大街上有一种智能垃圾桶,这种智能垃圾桶不仅可以供行人休息,灯箱边的中部还有USB接口可供行人充电.此种垃圾桶的侧面示意图如图所示,其中AC∥ED,AB∥EF∥GH,CD=20cm,DE=60cm,EF=100m,GH=80cm,∠CDE=∠EFG=90°,∠DEF=130°,则此种垃圾桶的高度(C到地面的距离)约为________cm.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
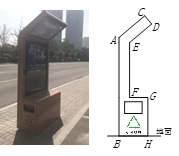
【答案】233.8
【解析】
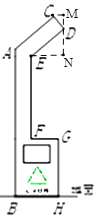
如图,过点E作EN⊥EF,过点D作MN⊥EN于N,过点C作CM⊥MN于M,可得∠DEN=40°,根据角的和差关系可得∠CDM=∠DEN=40°,利用∠CDM和∠DEN的三角函数可求出MD和DN的长,根据垃圾桶的高度为MD+DN+EF+GH即可得答案.
如图,过点E作EN⊥EF,过点D作MN⊥EN于N,过点C作CM⊥MN于M,
∴∠END=90°,∠M=90°,
∵∠DEF=130°,
∴∠DEN=∠DEF-90°=40°,
∵∠CDE=90°,
∴∠DEN+∠EDN=90°,∠CDM+∠EDN=90°,
∴∠CDM=∠DEN=40°,
∵CD=20cm,DE=60cm,
∴DM=CD·cos∠CDM≈20×0.77=15.4cm,DN=DE·sin∠DEN≈60×0.64=38.4cm,
∴DM+DN+EF+GH=15.4+38.4+80+100=233.8cm,
∴此种垃圾桶的高度约为233.8cm.
故答案为:233.8


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】某跳高集训队,对集训队员进行了一次跳高测试,经过统计,将集训队员的测试成绩(单位:m),绘制成尚不完整的扇形统计图(图①)与条形统计图(图②).
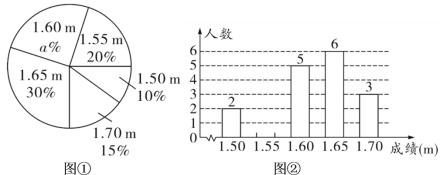
(1)![]() ________,请将条形统计图补充完整;
________,请将条形统计图补充完整;
(2)求集训队员测试成绩的众数;
(3)教练发现,测试成绩不包括两名请假的队员,补测后,把这两名队员的成绩(均是0.05的整数倍)与原测试成绩并成一组新数据,求新数据的中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
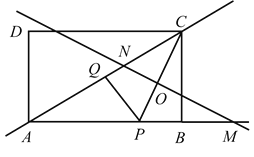
【题目】如图,矩形![]() 中,AB=8,BC=6,点
中,AB=8,BC=6,点![]() 是射线
是射线![]() 上一动点,设
上一动点,设![]() .过点
.过点![]() 做射线
做射线![]() 的垂线段
的垂线段![]() ,垂足为
,垂足为![]() ,作
,作![]() 的垂直平分线
的垂直平分线![]() 交射线
交射线![]() 于点
于点![]() ,交直线
,交直线![]() 于
于![]() .
.
![]() 点
点![]() 在边
在边![]() 上时.①用含
上时.①用含![]() 的代数式表示
的代数式表示![]() .②当
.②当![]() 时,直线ON交射线CD于
时,直线ON交射线CD于![]() ,求CE的长.
,求CE的长.
![]() 当
当![]() 为何值时,过
为何值时,过![]() 三点的圆与矩形
三点的圆与矩形![]() 的边或对角线
的边或对角线![]() 相切.
相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了锻炼学生身体素质,训练定向越野技能,某校在一公园内举行定向越野挑战赛.路线图如图![]() 所示,点
所示,点![]() 为矩形
为矩形![]() 边
边![]() 的中点,在矩形
的中点,在矩形![]() 的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员
的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 的路线匀速行进,到达点
的路线匀速行进,到达点![]() .设运动员
.设运动员![]() 的运动时间为
的运动时间为![]() ,到监测点的距离为
,到监测点的距离为![]() .现有
.现有![]() 与
与![]() 的函数关系的图象大致如图
的函数关系的图象大致如图![]() 所示,则这一信息的来源是( ).
所示,则这一信息的来源是( ).


A. 监测点![]() B. 监测点
B. 监测点![]() C. 监测点
C. 监测点![]() D. 监测点
D. 监测点![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
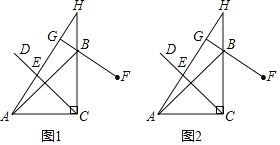
【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,E为∠ACB平分线CD上一动点(不与点C重合),点E关于直线BC的对称点为F,连接AE并延长交CB延长线于点H,连接FB并延长交直线AH于点G.
(1)求证:AE=BF.
(2)用等式表示线段FG,EG与CE的数量关系,并证明.
(3)连接GC,用等式表示线段GE,GC与GF的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
数学活动课上,老师让同学们根据如下问题情境,发现并提出问题.
如图1,△ABC与△EDC都是等腰直角三角形,点E,D分别在AC和BC上,连接EB.将线段EB绕点B顺时针旋转90°,得到的对应线段为BF.连接DF.“兴趣小组”提出了如下两个问题:①AE=BD,AE⊥BD;②DF=AB,DF⊥AB.
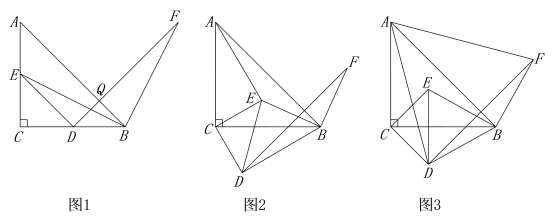
解决问题:
(1)请你证明“兴趣小组”提出的第②个问题.
探索发现:
(2)“实践小组”在图1的基础上,将△EDC绕点C顺时针旋转角度![]() (0°<
(0°<![]() <90°),其它条件保持不变,得到图2.
<90°),其它条件保持不变,得到图2.
①请你帮助“实践小组”探索:“兴趣小组”提出的两个问题是否还成立?如果成立,请给出证明;若不成立,请说明理由.
②如图3,当AD=AF时,请求出此时旋转角α的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
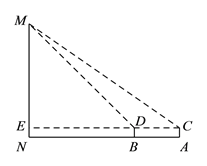
【题目】在北京市开展的“首都少年先锋岗”活动中,某数学小组到人民英雄纪念碑站岗执勤,并在活动后实地测量了纪念碑的高度. 方法如下:如图,首先在测量点A处用高为1.5m的测角仪AC测得人民英雄纪念碑MN顶部M的仰角为35°,然后在测量点B处用同样的测角仪BD测得人民英雄纪念碑MN顶部M的仰角为45°,最后测量出A,B两点间的距离为15m,并且N,B,A三点在一条直线上,连接CD并延长交MN于点E. 请你利用他们的测量结果,计算人民英雄纪念碑MN的高度.
(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
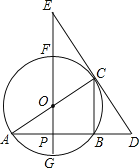
【题目】如图,⊙O中,FG、AC是直径,AB是弦,FG⊥AB,垂足为点P,过点C的直线交AB的延长线于点D,交GF的延长线于点E,已知AB=4,⊙O的半径为![]() .
.
(1)分别求出线段AP、CB的长;
(2)如果OE=5,求证:DE是⊙O的切线;
(3)如果tan∠E=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com