
【题目】综合与实践
问题情境
数学活动课上,老师让同学们根据如下问题情境,发现并提出问题.
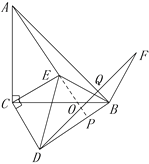
如图1,△ABC与△EDC都是等腰直角三角形,点E,D分别在AC和BC上,连接EB.将线段EB绕点B顺时针旋转90°,得到的对应线段为BF.连接DF.“兴趣小组”提出了如下两个问题:①AE=BD,AE⊥BD;②DF=AB,DF⊥AB.
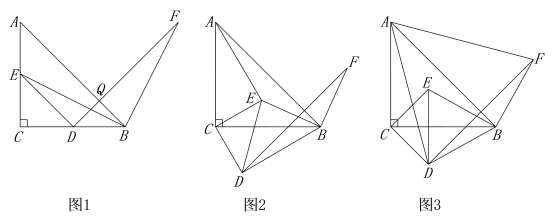
解决问题:
(1)请你证明“兴趣小组”提出的第②个问题.
探索发现:
(2)“实践小组”在图1的基础上,将△EDC绕点C顺时针旋转角度![]() (0°<
(0°<![]() <90°),其它条件保持不变,得到图2.
<90°),其它条件保持不变,得到图2.
①请你帮助“实践小组”探索:“兴趣小组”提出的两个问题是否还成立?如果成立,请给出证明;若不成立,请说明理由.
②如图3,当AD=AF时,请求出此时旋转角α的大小.
【答案】(1)见解析;(2)①成立,见解析;②45°
【解析】
(1)根据等腰直角三角形的性质及线段的和差关系可得AE=DB,由旋转的性质可得∠EBF=90°,BE=BF,根据三角形外角性质及角的和差关系可得∠AEB=∠DBF,利用SAS可证明△AEB≌△DBF,可得AB=DF,∠ABE=∠DFB,由∠ABE+∠ABF=90°可得∠DFB+∠ABF=90°,即可得出∠AQF=90°,可得AB⊥DF;
(2)①如图,延长AE与BD交于点P,交BC于O,根据旋转的性质可得∠ACE=∠DCB,利用SAS可证明△ACE≌△BCD,可得AE=BD,∠CAE=∠CBD,根据角的和差关系可得∠APB=90°,可得AE⊥BD;根据三角形外角性质及角的和差关系可得∠AEB=∠DBF,利用SAS可证明△AEB≌△DBF,可得AB=DF,∠ABE=∠DFB,由∠ABE+∠ABF=90°可得∠DFB+∠ABF=90°,即可得出∠AQF=90°,可得AB⊥DF;
②根据AD=AF,AB⊥DF可得AB垂直平分DF,可得BD=BF=BE,利用SSS可证明△BEC≌△BDC,可得∠DCB=∠ECB=![]() ∠ECD=45°,根据旋转的性质可得α=∠DCB=45°.
∠ECD=45°,根据旋转的性质可得α=∠DCB=45°.
(1)∵△ABC与△EDC为等腰直角三角形,
∴AC=BC,EC=DC,
∴AE=DB.
∵将线段EB绕点B顺时针旋转90°,得到的对应线段为BF,
∴∠EBF=90°,BE=BF,
∵∠AEB=∠C+∠EBC,∠DBF=∠EBF+∠DBE,∠C=∠EBF=90°,
∴∠AEB=∠DBF.
在△AEB和△DBF中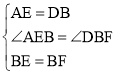 ,
,
∴△AEB≌△DBF,
∴AB=DF,∠ABE=∠DFB.
∵∠ABE+∠ABF=90°,
∴∠DFB+∠ABF=90°,
∴∠AQF=90°,即AB⊥DF.
(2)①如图,延长AE与BD交于点P,交BC于O,
∵将△EDC绕点C顺时针旋转角度![]()
∴∠ACE=∠DCB,
在△ACE和△BCD中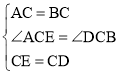 ,
,
∴△ACE≌△BCD,
∴AE=BD,∠CAE=∠CBD.
∵∠AOC=∠BOP,∠AOC+∠CAO=90°,
∴∠CBD+∠BOP=90°,
∴∠APB=90°,即AP⊥BD.
∵∠AEB=∠APB+∠EBD,∠DBF=∠EBF+∠DBE,∠APB=∠EBF=90°,
∴∠AEB=∠DBF.
在△AEB和△DBF中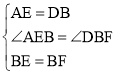 ,
,
∴△AEB≌△DBF,
∴AB=DF,∠ABE=∠DFB.
∵∠ABE+∠ABF=90°,
∴∠DFB+∠ABF=90°,
∴∠AQF=90°,即AB⊥DF.
②∵AD=AF,AB⊥DF,
∴AB垂直平分DF.
∴BD=BF=BE,
在△BEC和△BDC中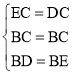 ,
,
∴△BEC≌△BDC,
∴∠DCB=∠ECB=![]() ∠ECD=45°.
∠ECD=45°.
∴旋转角α的大小是45°.


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
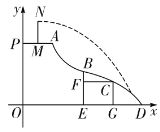
【题目】游乐园新建的一种新型水上滑道如图,其中线段![]() 表示距离水面(x轴)高度为5m的平台(点P在y轴上).滑道
表示距离水面(x轴)高度为5m的平台(点P在y轴上).滑道![]() 可以看作反比例函数图象的一部分,滑道
可以看作反比例函数图象的一部分,滑道![]() 可以看作是二次函数图象的一部分,两滑道的连接点B为二次函数
可以看作是二次函数图象的一部分,两滑道的连接点B为二次函数![]() 的顶点,且点B到水面的距离
的顶点,且点B到水面的距离![]() ,点B到y轴的距离是5m.当小明从上而下滑到点C时,与水面的距离
,点B到y轴的距离是5m.当小明从上而下滑到点C时,与水面的距离![]() ,与点B的水平距离
,与点B的水平距离![]() .
.
(1)求反比例函数的关系式及其自变量的取值范围;
(2)求整条滑道![]() 的水平距离;
的水平距离;
(3)若小明站在平台上相距y轴![]() 的点M处,用水枪朝正前方向下“扫射”,水枪出水口N距离平台
的点M处,用水枪朝正前方向下“扫射”,水枪出水口N距离平台![]() ,喷出的水流成抛物线形,设这条抛物线的二次项系数为p,若水流最终落在滑道
,喷出的水流成抛物线形,设这条抛物线的二次项系数为p,若水流最终落在滑道![]() 上(包括B、D两点),直接写出p的取值范围.
上(包括B、D两点),直接写出p的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与x轴交于点
与x轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)过第二象限的点![]() 作平行于x轴的直线,交直线
作平行于x轴的直线,交直线![]() 于点C,交函数
于点C,交函数![]() 的图象于点D.
的图象于点D.
①当![]() 时,判断线段PD与PC的数量关系,并说明理由;
时,判断线段PD与PC的数量关系,并说明理由;
②若![]() ,结合函数的图象,直接写出n的取值范围.
,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丁老师为了解所任教的两个班的学生数学学习情况,对数学进行了一次测试,获得了两个班的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.①A、B两班学生(两个班的人数相同)数学成绩不完整的频数分布直方图如下(数据分成 5 组:x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
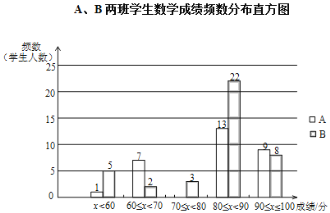
②A、B两班学生测试成绩在80≤x<90这一组的数据如下:
A 班:80 80 82 83 85 85 86 87 87 87 88 89 89
B 班:80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
③A、B两班学生测试成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
A班 | 80.6 | m | 96.9 |
B班 | 80.8 | n | 153.3 |
根据以上信息,请写出表中 m、n的值____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
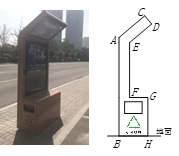
【题目】在太原迎泽西大街上有一种智能垃圾桶,这种智能垃圾桶不仅可以供行人休息,灯箱边的中部还有USB接口可供行人充电.此种垃圾桶的侧面示意图如图所示,其中AC∥ED,AB∥EF∥GH,CD=20cm,DE=60cm,EF=100m,GH=80cm,∠CDE=∠EFG=90°,∠DEF=130°,则此种垃圾桶的高度(C到地面的距离)约为________cm.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
查看答案和解析>>
科目:初中数学 来源: 题型:
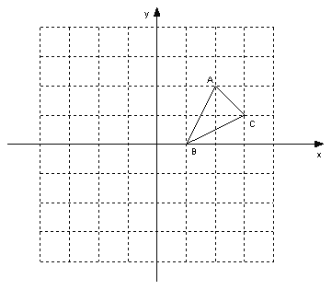
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)画出△ABC关于x轴对称的△A1B1C1,
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2,
(3)△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴并写出对称轴;
(4)△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全国初中数学联赛中,将参赛两个班学生的成绩(得分均为整数)进行整理后分成五组,绘制出如下的频率分布直方图(如图所示),已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.25、0.15、0.10、0.10,第二组的频数是40.
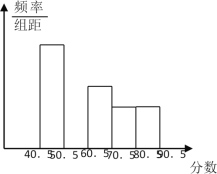
(1)第二小组的频率是_____,并补全这个频率分布直方图;
(2)这两个班参赛的学生人数是_________;
(3)这两个班参赛学生的成绩的中位数落在第______组内.(不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年4月23日是我国第一个“全民阅读日”某校开展了“建设书香校园,捐赠有益图书”活动.我们在参加活动的所有班级中,随机抽取了一个班,已知这个班是八年级5班,全班共50名学生.现将该班捐赠图书情况的统计结果,绘制成如下两幅不完整的统计图.
请你根据以上信息,解答下列问题:
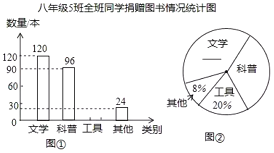
(1)补全上面的条形统计图和扇形统计图;
(2)求八年级5班平均每人捐赠了多少本书?
(3)若该校八年级共有800名学生,请你估算这个年级学生共可捐赠多少本书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:
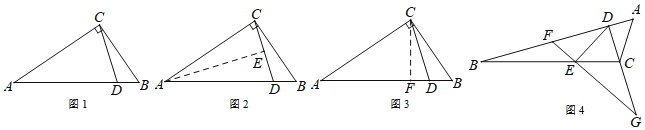
如图1,△ABC中,∠ACB=90°,点D在AB上,且∠BAC=2∠DCB,求证:AC=AD.
小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法1:如图2,作AE平分∠CAB,与CD相交于点E.
方法2:如图3,作∠DCF=∠DCB,与AB相交于点F.
(1)根据阅读材料,任选一种方法,证明AC=AD.
用学过的知识或参考小明的方法,解决下面的问题:
(2)如图4,△ABC中,点D在AB上,点E在BC上,且∠BDE=2∠ABC,点F在BD上,且∠AFE=∠BAC,延长DC、FE,相交于点G,且∠DGF=∠BDE.
①在图中找出与∠DEF相等的角,并加以证明;
②若AB=kDF,猜想线段DE与DB的数量关系,并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com