
����Ŀ����ȫ��������ѧ�����У�������������ѧ���ijɼ����÷־�Ϊ����������������ֳ����飬���Ƴ����µ�Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ������֪ͼ�д����ҵĵ�һ�����������ġ�����С���Ƶ�ʷֱ���0��25��0��15��0��10��0��10���ڶ����Ƶ����40��
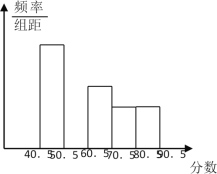
��1���ڶ�С���Ƶ����_____������ȫ���Ƶ�ʷֲ�ֱ��ͼ��
��2���������������ѧ��������_________��
��3�������������ѧ���ijɼ�����λ�����ڵ�______���ڣ�������˵�����ɣ�
���𰸡�0.4 100 ��
��������
��1��1��ȥ�������Ƶ�ʼ��ɣ�
��2���ڶ���Ƶ�����Եڶ���Ƶ�ʣ�
��3���ɵ�һ������Ƶ��֮��Ϊ0.25+0.4=0.65��0.5֪ǰ���������֮�ͳ���������������λ���Ķ������ɵã�
�⣺��1���ڶ�С��Ƶ��Ϊ1-��0.25+0.15+0.10+0.10��=0.4��
�ڶ���С���εĸ߶�ӦΪ�������4������ͼ��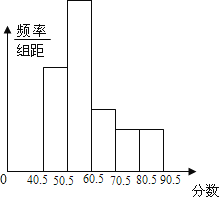
�ʴ�Ϊ��0.4��
��2���������������ѧ��������40��0.4=100�ˣ�
�ʴ�Ϊ��100��
��3���ߵ�һ������Ƶ��֮��Ϊ0.25+0.4=0.65��0.5��
����λ�����ڵڶ�С�飬
�ʴ�Ϊ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬����
���㣬����![]() ��
��![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() �������ߵĶԳ��ύ
�������ߵĶԳ��ύ![]() ���ڵ�
���ڵ�![]() ��ֱ��
��ֱ��![]() ������
������![]() ��
��![]() ������
������![]() ��
��
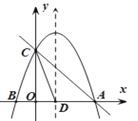
��1���������ߺ�ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2�����������ϴ���һ��![]() ��ʹ
��ʹ![]() �������
�������![]() �����2�������
�����2�������![]() �����ꣻ
�����ꣻ
��3���������ߵĶԳ������Ƿ����һ��![]() ��ʹ�߶�
��ʹ�߶�![]() ��
��![]() ��˳ʱ����ת
��˳ʱ����ת![]() �õ��߶�
�õ��߶�![]() ����
����![]() ǡ�������������ϣ������ڣ������
ǡ�������������ϣ������ڣ������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˶���ѧ���������ʣ�ѵ������ԽҰ���ܣ�ijУ��һ���ھ��ж���ԽҰ��ս����·��ͼ��ͼ![]() ��ʾ����
��ʾ����![]() Ϊ����
����![]() ��
��![]() ���е㣬�ھ���
���е㣬�ھ���![]() ���ĸ����㴦���ж�λ�ǣ��ɼ���˶�Ա��ԽҰ���̣�����һλ�˶�Ա
���ĸ����㴦���ж�λ�ǣ��ɼ���˶�Ա��ԽҰ���̣�����һλ�˶�Ա![]() �ӵ�
�ӵ�![]() ����������
����������![]() ��·�������н��������
��·�������н��������![]() �����˶�Ա
�����˶�Ա![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() ��������ľ���Ϊ
��������ľ���Ϊ![]() ������
������![]() ��
��![]() �ĺ�����ϵ��ͼ�������ͼ
�ĺ�����ϵ��ͼ�������ͼ![]() ��ʾ������һ��Ϣ����Դ�ǣ� ����
��ʾ������һ��Ϣ����Դ�ǣ� ����


A. ����![]() B. ����
B. ����![]() C. ����
C. ����![]() D. ����
D. ����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��
�����龳
��ѧ����ϣ���ʦ��ͬѧ�Ǹ������������龳�����ֲ�������⣮
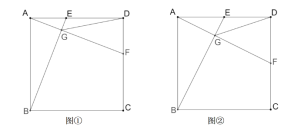
��ͼ1����ABC����EDC���ǵ���ֱ�������Σ���E��D�ֱ���AC��BC�ϣ�����EB�����߶�EB�Ƶ�B˳ʱ����ת90�����õ��Ķ�Ӧ�߶�ΪBF������DF������ȤС�顱����������������⣺��AE=BD��AE��BD����DF=AB��DF��AB��
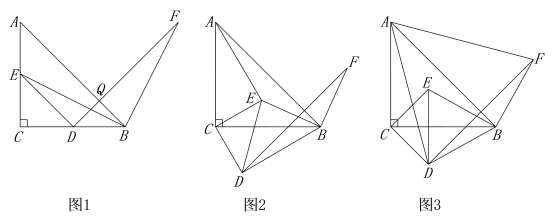
������⣺
��1������֤������ȤС�顱����ĵڢڸ����⣮
̽�����֣�
��2����ʵ��С�顱��ͼ1�Ļ����ϣ�����EDC�Ƶ�C˳ʱ����ת�Ƕ�![]() ��0����
��0����![]() ��90�����������������ֲ��䣬�õ�ͼ2��
��90�����������������ֲ��䣬�õ�ͼ2��
�����������ʵ��С�顱̽��������ȤС�顱��������������Ƿ�������������������֤����������������˵�����ɣ�
����ͼ3����AD=AFʱ���������ʱ��ת�����Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
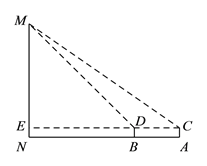
����Ŀ���ڱ����п�չ�����������ȷ������У�ij��ѧС�鵽����Ӣ�ۼ��վ��ִ�ڣ����ڻ��ʵ�ز����˼���ĸ߶�. �������£���ͼ�������ڲ�����A���ø�Ϊ1.5m�IJ����AC�������Ӣ�ۼ��MN����M������Ϊ35����Ȼ���ڲ�����B����ͬ���IJ����BD�������Ӣ�ۼ��MN����M������Ϊ45������������A��B�����ľ���Ϊ15m������N��B��A������һ��ֱ���ϣ�����CD���ӳ���MN�ڵ�E. �����������ǵIJ����������������Ӣ�ۼ��MN�ĸ߶�.
���ο����ݣ�sin35���0.6��cos35���0.8��tan35���0.7��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У������ꡢ�����궼Ϊ�����ĵ��Ϊ���㣮����۲�ͼ��������A1B1C1D1��A2B2C2D2��A3B3C3D3��ÿ���������������ϵ�����ĸ��������˹��������������A10B10C10D10�������ϵ����㹲��______����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
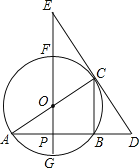
����Ŀ����ͼ����O�У�FG��AC��ֱ����AB���ң�FG��AB������Ϊ��P������C��ֱ�߽�AB���ӳ����ڵ�D����GF���ӳ����ڵ�E����֪AB=4����O�İ뾶Ϊ![]() ��
��
��1���ֱ�����߶�AP��CB�ij���
��2�����OE=5����֤��DE����O�����ߣ�
��3�����tan��E=![]() ����DE�ij���
����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �߳�Ϊ2��
�߳�Ϊ2��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �������㣬������
�������㣬������![]() ,
,![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
��1����ͼ1,�ж��߶�![]() ��
��![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
��2���ڣ�1���������£�����![]() ,ֱ��д��
,ֱ��д��![]() ����СֵΪ ��
����СֵΪ ��
��3����ͼ2����![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() ��
��
����֤��![]() ƽ��
ƽ��![]() ��
��
�����߶�![]() �ij��ȣ�
�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC�Ķ�������ΪA����4��1����B����2��3����C����1��2����
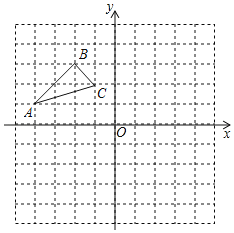
��1��������ABC����ԭ��O�����ĶԳƵ���A��B��C������A����B����C���ֱ��ǵ�A��B��C�Ķ�Ӧ�㣮
��2�������B���ķ�������������ʽ��
��3���ж�A��B�����е�P�Ƿ��ڣ�2���ĺ���ͼ���ϣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com