
【题目】如图,小平为了测量学校教学楼的高度,她先在A处利用测角仪测得楼顶C的仰角为30°,再向楼的方向直行50米到达B处,又测得楼顶C的仰角为60度.已知测角仪的高度是1.2米,请你帮助小平计算出学校教学楼的高度CO.(![]() )
)
科目:初中数学 来源: 题型:
【题目】骰子是一种特别的数字立方体(见右图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )
![]()
A.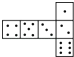 B.
B.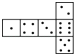 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
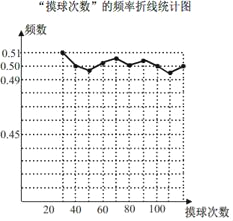
【题目】在一个不透明袋子中装有颜色不同的黑、白两种球共40个球,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.如图是“摸到白球”的频率折线统计图:
(1)根据统计图,估算盒子里黑、白两种颜色的球各多少个?
(2)如果要使摸到白球的概率为![]() ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形;②△HED的面积是1﹣![]() ;③∠AFG=112.5°;④BC+FG=
;③∠AFG=112.5°;④BC+FG=![]() .其中正确的结论是( )
.其中正确的结论是( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李按市场价格30元/千克收购了一批海鲜1000千克存放在冷库里,据预测,海鲜的市场价格将每天每千克上涨1元.冷冻存放这批海鲜每天需要支出各种费用合计310元,而且这些海鲜在冷库中最多存放160天,同时平均每天有3千克的海鲜变质.
(1)设x天后每千克该海鲜的市场价格为y元,试写出y与x之间的函数关系式;
(2)若存放x天后,将这批海鲜一次性出售.设这批海鲜的销售总额为P元,试写出P与x之间的函数关系式;
(3)小李将这批海鲜存放多少天后出售可获得最大利润,最大利润是多少元?(利润W=销售总额﹣收购成本﹣各种费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B分别在y轴和x轴上,∠ABO=60°,在坐标轴上找一点P,使得△PAB是等腰三角形,则符合条件的点P共有( )
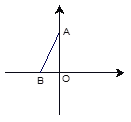
A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A、B两种上网学习的月收费方案:
A方案:月租7元,可上网25小时,若超时,超出部分按每分钟0.01元收费;
B方案:月租10元,可上网50小时,若超时,超出部分按每分钟0.01元收费;
设每月上网学习时间为![]() 小时.
小时.
(1)当![]() >50时,用含有x的代数式分别表示A、B两种上网的费用;
>50时,用含有x的代数式分别表示A、B两种上网的费用;
(2)当x=100时,分别求出两种上网学习的费用.
(3)若上网40小时,选择哪种方式上网学习合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△CDE都是等腰直角三角形,∠C=90°,将△CDE绕点C逆时针旋转一个角度α(0°<α<90°),使点A,D,E在同一直线上,连接AD,BE.
(1)①依题意补全图2;
②求证:AD=BE,且AD⊥BE;
③作CM⊥DE,垂足为M,请用等式表示出线段CM,AE,BE之间的数量关系;
(2)如图3,正方形ABCD边长为![]() , 若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
, 若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com