Question

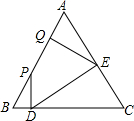
15．如图，等边△ABC的边长是4，点P是边AB上任意一点（可与A、B重合），作PD⊥BC于D，作DE⊥AC于E，作EQ⊥AB于Q，设PB的长为x，PQ的长为y，则y与x的函数关系图象是（　　）

• A．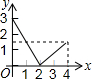
• B．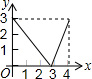
• C．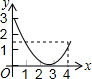
• D．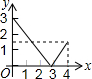

Answer 1

分析 根据题意，等边△ABC的边长是4，PB的长为x，则BD=$\frac{x}{2}$，CD=4-$\frac{x}{2}$，CE=$\frac{1}{2}$（4-$\frac{x}{2}$）=2-$\frac{x}{4}$，AE=4-（2-$\frac{x}{4}$）=2+$\frac{x}{4}$，AQ=$\frac{1}{2}$（2+$\frac{x}{4}$）=1+$\frac{x}{8}$，所以当P在Q下方时，y=AB-PB-AQ，当P在Q上方时，y=AQ-AP，列出函数表达式即可作出判断．

解答 解：∵等边△ABC的边长是4，PB的长为x，PD⊥BC于D，DE⊥AC于E，EQ⊥AB于Q，
∴∠PDB=∠DEC=∠EQA=90°，∠PBD=∠CDE=∠AEQ=30°，
∴BD=$\frac{x}{2}$，CD=4-$\frac{x}{2}$，CE=$\frac{1}{2}$（4-$\frac{x}{2}$）=2-$\frac{x}{4}$，AE=4-（2-$\frac{x}{4}$）=2+$\frac{x}{4}$，AQ=$\frac{1}{2}$（2+$\frac{x}{4}$）=1+$\frac{x}{8}$，
∴当P在Q下方时，y=AB-PB-AQ=4-x-（1+$\frac{x}{8}$）=-$\frac{x}{8}$+3，
当P在Q上方时，y=AQ-AP=（1+$\frac{x}{8}$）-（4-x）=$\frac{9}{8}$x-3，
当y=0时，x=$\frac{8}{3}$，当x=0时，y=3，当x=4时，y=$\frac{3}{2}$，
∴y=$\left\{\begin{array}{l}{-\frac{x}{8}+3（0≤x≤\frac{8}{3}）}\\{\frac{9}{8}x-3（\frac{8}{3}＜x≤4）}\end{array}\right.$
故选：D．

点评 本题考查了函数的图象，能够根据题意列出函数表达式是对函数图象做出正确判断的关键所在．