
【题目】如图,已知锐角△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.
(1)求证:MN⊥DE.
(2)连结DM,ME,猜想∠A与∠DME之间的关系,并证明猜想.

(3)当∠A变为钝角时,如图,上述(1)(2)中的结论是否都成立, 若结论成立,直接回答,不需证明;若结论不成立,说明理由.

【答案】(1)证明见解析;(2)∠DME=180°-2∠A,理由见解析;(3)结论(1)成立, 结论(2)不成立.
【解析】试题分析:
(1)如图,连接DM、ME,由CD、BE是△ABC的高可得∠BDC=∠BEC=90°,结合点M是BC的中点,可得ME=![]() BC,MD=
BC,MD=![]() BC,由此可得ME=MD,再结合点N是DE的中点,利用等腰三角形的“三线合一”可得:MN⊥DE;
BC,由此可得ME=MD,再结合点N是DE的中点,利用等腰三角形的“三线合一”可得:MN⊥DE;
(2)由(1)可知:DM=ME=BM=MC,则:∠DBM=∠BDM,∠ECM=∠CEM,由此可得:∠DMB=180°-2∠DBM,∠EMC=180°-2∠ECM,结合∠DME=180°-∠DMB-∠EMC可得∠DME=2(∠DBM+∠ECM)-180°,再结合:∠DBM+∠ECM=180°-∠A可得∠DME=180°-2∠A;
(3)①同(1)中思路一样可证得在当∠A为钝角时,原来(1)中的结论成立;② 当∠A为钝角时,由①可知,DM=ME=BM=MC,则∠MCE=∠MEC,∠MBD=∠MDB,由此可得∠BME=∠MEC+∠MCE=2∠MCE,∠CMD=∠MBD+∠MDB=2∠MBD,结合∠DME=180°-∠BME-∠CMD,可得∠DME=180°-2(∠MBD+∠MCE),再结合∠MBD+∠MCE)=180°-∠A可得∠DME=2∠A-180°,从而可得原(2)中的结论不成立.

试题解析:
(1)如图,连接DM,ME,
∵CD、BE分别是AB、AC边上的高,M是BC的中点,
∴DM=![]() BC,ME=
BC,ME=![]() BC,
BC,
∴DM=ME,
又∵N为DE中点,
∴MN⊥DE;
(2)在△ABC中,∠ABC+∠ACB=180°-∠A,
∵DM=ME=BM=MC,
∴∠DBM=∠BDM,∠ECM=∠CEM,
∴∠BMD=180°-2∠DBM,∠CME=180°-2∠ECM,
∴∠BMD+∠CME=(180°-2∠ABC)+(180°-2∠ACB)=360°-2(∠ABC+∠ACB)=360°-2(180°-∠A)=2∠A,
∴∠DME=180°-2∠A;
(3)结论(1)成立, 结论(2)不成立,
理由如下:
①如图,连接DM,ME,
∵CD、BE分别是AB、AC边上的高,M是BC的中点,
∴DM=![]() BC,ME=
BC,ME=![]() BC,
BC,
∴DM=ME,
又∵N为DE中点,
∴MN⊥DE;
②由①可知,DM=ME=BM=MC,
∴∠MCE=∠MEC,∠MBD=∠MDB,
∴∠BME=∠MEC+∠MCE=2∠MCE,∠CMD=∠MBD+∠MDB=2∠MBD,
又∵∠DME=180°-∠BME-∠CMD,
∴∠DME=180°-2(∠MBD+∠MCE),
又∵在△ABC中,∠MBD+∠MCE=180°-∠BAC
∴∠DME=180°-2(180°-∠BAC)=2∠BAC-180°.
∴(2)中原来的结论不成立.



 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】(满分8分) 已知:如图,在正方形ABCD中,F是AB上一点,延长CB到E,使BE=BF,连接CF并延长交AE于G.
(1)求证:△ABE≌△CBF;
(2)将△ABE绕点A逆时针旋转90°得到△ADH,请判断四边形AFCH是什么特殊四边形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
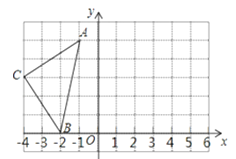
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣2,0),C(﹣4,3).
(1)请画出△ABC关于y轴对称的△A'B′C′(其中A'、B′、C′分别是A、B、C的对称点,不写画法);
(2)写出C′的坐标,并求△ABC的面积;
(3)在y轴上找出点P的位置,使线段PA+PB的最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com