
����Ŀ����ͼ����ƽ��ֱ������ϵxoy�У�ֱ��y= ![]() x+2��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c�ĶԳ�����x=��
x+2��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c�ĶԳ�����x=�� ![]() ���Ҿ���A��C���㣬��x�����һ������Ϊ��B��
���Ҿ���A��C���㣬��x�����һ������Ϊ��B��
��1���������߽���ʽ��
��2������PΪֱ��AC�Ϸ����������ϵ�һ�㣬����PA��PC�����ı���PAOC����������ֵ���������ʱ��P�����꣮
��3�����������Ƿ���ڵ�M������M��MN��ֱx���ڵ�N��ʹ���Ե�A��M��NΪ��������������AOC���ƣ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺y= ![]() x+2�У���x=0ʱ��y=2����y=0ʱ��x=��4��
x+2�У���x=0ʱ��y=2����y=0ʱ��x=��4��
��C��0��2����A����4��0����
�������ߵĶԳ��Կ�֪����A���B����x=�� ![]() �Գƣ�
�Գƣ�
���B������Ϊ1��0����
��������y=ax2+bx+c��A����4��0����B��1��0����
����������߽���ʽΪy=a��x+4����x��1����
�֡������߹���C��0��2����
��2=��4a
��a=�� ![]()
��y=�� ![]() x2��
x2�� ![]() x+2��
x+2��
��2��
�⣺��P��m���� ![]() m2��
m2�� ![]() m+2����
m+2����
��ͼ1������P��PQ��x�ύAC�ڵ�Q��

��Q��m�� ![]() m+2����
m+2����
��PQ=�� ![]() m2��
m2�� ![]() m+2����
m+2���� ![]() m+2��
m+2��
=�� ![]() m2��2m��
m2��2m��
��S�ı���PAOC=S��AOC+S��PAC= ![]() ��4��2+
��4��2+ ![]() ��PQ��4=2PQ+4=��m2��4m+4=����m+2��2+8��
��PQ��4=2PQ+4=��m2��4m+4=����m+2��2+8��
�൱m=��2ʱ����PAC����������ֵ��8��
��ʱP����2��3����
��3��
�⣺��ͼ2��
 ��
��
��Rt��AOC��AC= ![]() =2
=2 ![]() ����Rt��BOC��BC=
����Rt��BOC��BC= ![]() =
= ![]() ��
��
��AC2+BC2=20+5=25=AB2��
���ACB=90�㣬CO��AB��
���ABC�ס�AOC�ס�CBO��
������M��x���Ϸ�ʱ����M����C���غϣ���M��0��2��ʱ����MAN�ס�BAC��
���������ߵĶԳ��ԣ���M����3��2��ʱ����MAN�ס�ABC��
������M��x����·�ʱ����N��n��0������M��n���� ![]() n2��
n2�� ![]() n+2����
n+2����
��MN= ![]() n2+
n2+ ![]() n��2��AN=n+4��
n��2��AN=n+4��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() =
= ![]() =
= ![]() ʱ��MN=
ʱ��MN= ![]() AN����
AN���� ![]() n2+
n2+ ![]() n��2=
n��2= ![]() ��n+4����
��n+4����
����n2+2n��8=0��
n1=��4���ᣩ��n2=2��M��2����3����
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() =
= ![]() =2ʱ��MN=2AN����
=2ʱ��MN=2AN���� ![]() n2+
n2+ ![]() n��2=2��n+4����
n��2=2��n+4����
����n2��n��20=0��
��ã�n1=��4����ȥ����n2=5��
��M��5����18����
�������������ڵ�M1��0��2����M2����3��2����M3��2����3����M4��5����18����ʹ���Ե�A��M��NΪ��������������ABC���ƣ�
����������1�������ֱ��y= ![]() x+2��x�ύ������꣬Ȼ�����������ߵĶԳ��Կ���õ�B�����ꣻ�������ߵĽ���ʽΪy=y=a��x+4����x��1����Ȼ��C��������뼴�����a��ֵ����2�����P��Q�ĺ�����Ϊm���ֱ���õ�P��Q�������꣬�Ӷ��ɵõ��߶�PQ=
x+2��x�ύ������꣬Ȼ�����������ߵĶԳ��Կ���õ�B�����ꣻ�������ߵĽ���ʽΪy=y=a��x+4����x��1����Ȼ��C��������뼴�����a��ֵ����2�����P��Q�ĺ�����Ϊm���ֱ���õ�P��Q�������꣬�Ӷ��ɵõ��߶�PQ= ![]() m2��2m��Ȼ�����������ε������ʽ�����S�ı���PAOC=S��AOC+S��PAC=2PQ+4��Ȼ�������䷽������á�PAC����������ֵ�Լ���ʱm��ֵ���Ӷ�����õ�P�����ꣻ��3�����������Ƕ�Ӧ��ȵ��������������ƣ��ɵ�M1 �� ���������ߵĶԳ��ԣ��ɵ�M2 �� ���ݶ�Ӧ�߳ɱ����Ҽн���ȵ��������������ƣ��ɵù���n�ķ��̣����ݽⷽ�̣��ɵô𰸣�
m2��2m��Ȼ�����������ε������ʽ�����S�ı���PAOC=S��AOC+S��PAC=2PQ+4��Ȼ�������䷽������á�PAC����������ֵ�Լ���ʱm��ֵ���Ӷ�����õ�P�����ꣻ��3�����������Ƕ�Ӧ��ȵ��������������ƣ��ɵ�M1 �� ���������ߵĶԳ��ԣ��ɵ�M2 �� ���ݶ�Ӧ�߳ɱ����Ҽн���ȵ��������������ƣ��ɵù���n�ķ��̣����ݽⷽ�̣��ɵô𰸣�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC����DCE����FEG������ȫ�ȵĵ��������Σ��ױ�BC��CE��EG��ͬһֱ���ϣ���AB= ![]() ��BC=1������BF���ֱ�AC��DC��DE�ڵ�P��Q��R��
��BC=1������BF���ֱ�AC��DC��DE�ڵ�P��Q��R��
��1����֤����BFG�ס�FEG�������BF�ij���
��2����AP��PC��ֵ��
��3���۲�ͼ�Σ��������һ�����P��ص����⣬�����н�𣮣������������IJ�κͽ�����ƽ�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������꼶����������ʵ����ijɼ������������ֳ�5��С�飨x��ʾ�ɼ�����λ���ף���A�飺5.25��x��6.25��B�飺6.25��x��7.25��C�飺7.25��x��8.25��D�飺8.25��x��9.25��E�飺9.25��x��10.25�������Ƴ�����ͳ��ͼ��Ƶ���ֲ�ֱ��ͼ�������������涨x��6.25Ϊ�ϸ�x��9.25Ϊ���㣮 
��1���ⲿ�������ж����ˣ����гɼ��ϸ���ж����ˣ�
��2���ⲿ�������ɼ�����λ��������һ�飿����ͳ��ͼ��D���Ӧ��Բ�Ľ��Ƕ��ٶȣ�
��3��Ҫ�ӳɼ������ѧ���У����ѡ��2�˽��ܾ��飬��֪�ס�����λͬѧ�ijɼ���Ϊ���㣬������������1�˱�ѡ�еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������y1= ![]() ��һ�κ���y2=k2x+b��ͼ���ڵ�A��1��8����B����4��m�����㣮
��һ�κ���y2=k2x+b��ͼ���ڵ�A��1��8����B����4��m�����㣮 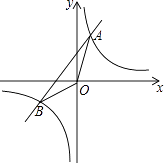
��1����k1 �� k2 �� b��ֵ��
��2�����AOB�������
��3����ֱ��д������ʽ ![]() x+b�Ľ⣮
x+b�Ľ⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCD�У���E��F�ֱ���AB��CD�ϣ���AE=CF�� 
��1����֤����ADE�ա�CBF��
��2����DF=BF����֤���ı���DEBFΪ���Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����BE��AC��CE��BD�� 
��1����֤���ı���OBEC�Ǿ��Σ�
��2��������ABCD���ܳ���4 ![]() ��tan��=
��tan��= ![]() �����ı���OBEC�������
�����ı���OBEC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ı���ABCD�У�AD=DC����DAB=��ACB=90�㣬����D��DF��AC������ΪF��DF��AB�ཻ��E����AB=15��BC=9��P������DF�ϵĶ��㣮����BCP���ܳ���Сʱ��DP�ij�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCD�ڵ�һ�����ڣ���BC��x��ƽ�У�A��B�����������ֱ�Ϊ3��1������������y= ![]() ��ͼ��A��B���㣬������ABCD�����Ϊ ��
��ͼ��A��B���㣬������ABCD�����Ϊ �� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com