
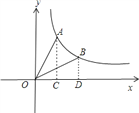
【题目】在平面直角坐标系中,已知反比例函数y=![]() 的图象经过点A(1,
的图象经过点A(1, ![]() ).连接OA,将线段OA绕O点顺时针旋转30°得到线段OB,判断点B是否在此反比例函数的图象上,并说明理由.
).连接OA,将线段OA绕O点顺时针旋转30°得到线段OB,判断点B是否在此反比例函数的图象上,并说明理由.
【答案】点B在此反比例函数的图象上.理由见解析.
【解析】试题分析:根据反比例函数图象上点的坐标特征计算k的值,过点A作x轴的垂线交x轴于点C,过点B作x轴的垂线交x轴于点D,在Rt△AOC中,根据勾股定理计算出OA=2,利用含30度的直角三角形三边的关系得到∠OAC=30°,则∠AOC=60°,再根据旋转的性质得∠AOB=30°,OB=OA=2,所以∠BOD=30°,在Rt△BOD中,计算出BD=![]() OB=1,OD=
OB=1,OD=![]() BD=
BD=![]() ,于是得到B点坐标为(
,于是得到B点坐标为(![]() ,1),然后根据反比例函数图象上点的坐标特征判断B点在反比例函数图象上.
,1),然后根据反比例函数图象上点的坐标特征判断B点在反比例函数图象上.
试题解析:
点B在此反比例函数的图象上.
理由如下:
把A(1, ![]() )代入y=
)代入y=![]() ,得k=1×
,得k=1×![]() =
=![]() ,
,
∴反比例函数的解析式为y=![]() .
.
过点A作AD⊥x轴,垂足为点D.
∵点A的坐标为(1, ![]() ),
),
∴OD=1,AD=![]() ,
,
∴OA=![]() =2,
=2,
∴∠OAD=30°,
∴∠AOD=60°.
过点B作BC⊥x轴,垂足为点C.
∵∠AOB=30°,
∴∠BOC=∠AOD-∠AOB=30°.
∵OB=OA=2,
∴BC=1,
∴OC=![]() =
=![]() ,
,
∴点B的坐标为(![]() ,1),
,1),
∴点B在此反比例函数的图象上.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,分别位于反比例函数y=![]() ,y=
,y=![]() 在第一象限图象上的两点A,B,与原点O在同一直线上,且
在第一象限图象上的两点A,B,与原点O在同一直线上,且![]() .
.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)过点A作x轴的平行线交y=![]() 的图象于点C,连接BC,求△ABC的面积.
的图象于点C,连接BC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D
(1)求证:△BFD∽△ABD;
(2)求证:DE=DB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,在△ABC中,点O是AC上一点,过点O的直线与AB,BC的延长线分别相交于点M,N.
【问题引入】
(1)若点O是AC的中点, ![]() ,求
,求![]() 的值;
的值;
温馨提示:过点A作MN的平行线交BN的延长线于点G.
【探索研究】
(2)若点O是AC上任意一点(不与A,C重合),求证: ![]() ;
;
【拓展应用】
(3)如图②所示,点P是△ABC内任意一点,射线AP,BP,CP分别交BC,AC,AB于点D,E,F.若![]() ,
, ![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】火星和地球的距离约为34 000 000千米,用科学记数法表示34 000 000的结果是( )千米.
A.0.34×108
B.3.4×106
C.34×106
D.3.4×107
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com