

���� ��1����a2+2a=x����ԭʽ���κ�������뼴�ɣ�
��2����������ڱ���Ϊ���Ƣٵ���ʽ������$\frac{1}{4}$x=m��$\frac{1}{2}$y=n���ɢٵã�$\left\{\begin{array}{l}{m=1}\\{n=3}\end{array}\right.$ ��$\left\{\begin{array}{l}{x=4}\\{y=6}\end{array}\right.$��
��3����x+2=a��y+1=b����ԭ��������������ⷽ���鼴�ɣ�
��4������ʽ������߱���Ϊ��Ϊ��������ʽ���ó����ۣ����x��ֵ��
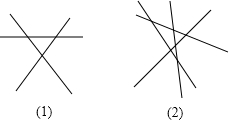
��5����ͼ��1����������ֱ�߱�������ֱ�����أ��ó�ͬ���ڽǵĶ��������ֿ����γ�6��ͬ���ڽǣ���ͼ��2�������ݣ�1���еĽ��۵ó���
������Ǩ�ơ�д��һ��ʽ�ӣ����ֽ���ʽ����a+b����һ�����壬ȥ���ţ�������ȫƽ����ʽ��ʽ�ֽ⣮
��� �⣺��1����a2+2a=x��
��5-4a-2a2��=5-2��a2+2a��=5-2x=5-2��5=-5��
�ʴ�Ϊ��-5��
��2��$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$�٣�$\left\{\begin{array}{l}{{a}_{1}x+2{b}_{1}y=4{c}_{1}}\\{{a}_{2}x+2{b}_{2}y=4{c}_{2}}\end{array}\right.$�ڣ�
���ڱ��εã�$\left\{\begin{array}{l}{{a}_{1}•\frac{1}{4}x+{b}_{1}•\frac{1}{2}y={c}_{1}}\\{{a}_{2}•\frac{1}{4}x+{b}_{2}•\frac{1}{2}y={c}_{2}}\end{array}\right.$�ۣ�
��$\frac{1}{4}$x=m��$\frac{1}{2}$y=n��
����ۿɻ�Ϊ��$\left\{\begin{array}{l}{{a}_{1}m+{b}_{1}n={c}_{1}}\\{{a}_{2}m+{b}_{2}n={c}_{2}}\end{array}\right.$�ܣ�
�ȽϷ�����ٺܵ͢�$\left\{\begin{array}{l}{m=1}\\{n=3}\end{array}\right.$ ��$\left\{\begin{array}{l}{x=4}\\{y=6}\end{array}\right.$��
�����ڵĽ�Ϊ��$\left\{\begin{array}{l}{x=4}\\{y=6}\end{array}\right.$��
�ʴ�Ϊ��$\left\{\begin{array}{l}{x=4}\\{y=6}\end{array}\right.$��
��3����x+2=a��y+1=b��
��ԭ���������Ϊ��$\left\{\begin{array}{l}{2013a+2014b=1��}\\{2014a+2013b=-1��}\end{array}\right.$��
��+�ڵã�a+b=0�ۣ�
��-�ٵã�a-b=-2�ܣ�
�ɢۺ͢�����µķ�����Ϊ$\left\{\begin{array}{l}{a+b=0}\\{a-b=-2}\end{array}\right.$ ���$\left\{\begin{array}{l}{a=-1}\\{b=1}\end{array}\right.$��
��$\left\{\begin{array}{l}{x=-3}\\{y=0}\end{array}\right.$��
�ʴ�Ϊ��$\left\{\begin{array}{l}{x=-3}\\{y=0}\end{array}\right.$��
��4��x+$\frac{1}{x-1}$=a+$\frac{1}{a-1}$��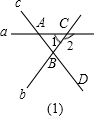
x-1+$\frac{1}{x-1}$=a-1+$\frac{1}{a-1}$��
��x-1=a-1��x-1=$\frac{1}{a-1}$��
��x1=a��x2=$\frac{a}{a-1}$��
�����飺x1=a��x2=$\frac{a}{a-1}$��ԭ���̵Ľ⣻
�ʴ�Ϊ��x1=a��x2=$\frac{a}{a-1}$��
��5����ͼ��1����ֱ��a��ֱ��c��ֱ��b����ʱ�������ɵ�ͬ���ڽ��У���1���ABC����2���CBD��
ͬ����ÿһ��ֱ��������ʱ����������ͬ���ڽǣ�����һ����6��ͬ���ڽǣ�
��ͼ2��������ͬһ�������ֱ�������ཻ����������ֱ�߷ֱ�Ϊa��b��c��d�����Է�Ϊ��a��b��c����a��b��d����a��c��d����b��c��d��ÿ����ֱ�߶�������6��ͬ���ڽǣ���������������һ����24��ͬ���ڽǣ�
�ʴ�Ϊ��6��24��
������Ǩ�ơ�
��ʽ�ֽ⣺��a+b����a+b-4��+4��
�⣺ԭʽ=��a+b��2-4��a+b��+4��
=��a+b-2��2��
���� �����Ǹ����Ķ����Ͻ��ʵ�����⣬���õ�֪ʶ�Ƚ϶࣬���ѶȲ�����������ֵ������������˼�룬������ѧ����о������ã���������������˼�룬����Ӧ���ڽⷽ�̻��飬Ҳ�����������������ֵ����ʽ�ֽ⣬ͬʱ�ڼ���ͼ����Ҳ�����ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����ʦ����������ѧϰ�����мס���������վ������ʦѡ����֪����վ���շѷ�ʽ�ǣ���ʹ�÷�7Ԫ����ʱ����ʱ��25Сʱ����ʱ��ÿ����0.01Ԫ�� ����վ�����շѷ�ʽ��ͼ��ʾ��������ʦÿ��������ʱ��ΪxСʱ���ס���������վ�����շѽ��ֱ���y1��y2��
����ʦ����������ѧϰ�����мס���������վ������ʦѡ����֪����վ���շѷ�ʽ�ǣ���ʹ�÷�7Ԫ����ʱ����ʱ��25Сʱ����ʱ��ÿ����0.01Ԫ�� ����վ�����շѷ�ʽ��ͼ��ʾ��������ʦÿ��������ʱ��ΪxСʱ���ס���������վ�����շѽ��ֱ���y1��y2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�D��BC�ߵ��е㣬F��E�ֱ���AD�����ӳ����ϵĵ㣬CF��BE������BF��CE��
��ͼ���ڡ�ABC�У�D��BC�ߵ��е㣬F��E�ֱ���AD�����ӳ����ϵĵ㣬CF��BE������BF��CE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����O��ֱ��AB����һ�㣬����OD������OE�ֱ�ƽ�֡�AOC�͡�BOC��
��ͼ����O��ֱ��AB����һ�㣬����OD������OE�ֱ�ƽ�֡�AOC�͡�BOC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �ɼ����֣� | 50 | 60 | 70 | 80 | 90 |
| �������ˣ� | 1 | 4 | x | y | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com