
【题目】已知方程x2+2kx+k2-2k+1=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)若![]() =4,求k的值.
=4,求k的值.
科目:初中数学 来源: 题型:
【题目】某景区在“五一”小长假期间,每天接待的旅客人数统计如下表.
日期 | 5月1日 | 5月2日 | 5月3日 | 5月4日 | 5月5日 |
人数(万人) | 1.2 | 2 | 2.5 | 2 | 1.1 |
表中表示人数的一组数据中,众数和中位数分别为( )
A.2.5万,2万B.2.5万,2.5万C.2万,2.5万D.2万,2万
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC,交直线m于点E,垂足为点F,连接CD,BE.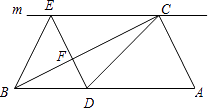
(1)求证:CE=AD;
(2)当点D是AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)当∠A的大小满足什么条件时,四边形BECD是正方形?(不需要证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中|a+1|+(b﹣![]() )2=0.
)2=0.
(2)先化简,再求值:﹣(3x2﹣4xy)﹣![]() [x2﹣2(4x﹣4xy)],其中x=﹣2.
[x2﹣2(4x﹣4xy)],其中x=﹣2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com