
【题目】如图,BD与CD分别平分∠ABC,∠ACB的外角∠EBC,∠FCB,若∠A=80°,则∠BDC= . 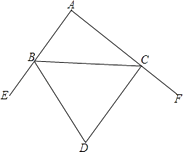
【答案】50°
【解析】证明:BD、CD分别是∠CBE、∠BCF的平分线
∴∠DBC= ![]() ∠EBC,∠BCD=
∠EBC,∠BCD= ![]() ∠BCF,
∠BCF,
∵∠CBE、∠BCF是△ABC的两个外角
∴∠CBE+∠BCF=360°﹣(180°﹣∠A)=180°+∠A=260°,
∴∠DBC+∠BCD= ![]() (∠EBC+∠BCF)=130°
(∠EBC+∠BCF)=130°
在△DBC中,∠BDC=180°﹣(∠DBC+∠BCD)=180°﹣130°=50°,
所以答案是:50°.
【考点精析】利用三角形的内角和外角和三角形的外角对题目进行判断即可得到答案,需要熟知三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


科目:初中数学 来源: 题型:
【题目】【问题情境】:
如图1,AB//CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE//AB,通过平行线性质来求∠APC.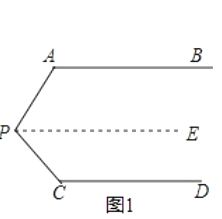
(1)按小明的思路,求∠APC的度数;
(2)【问题迁移】:
如图2,AB//CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)【问题应用】:
在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组数中,具有相反意义的量是( )
A.身高180cm和身高90cm
B.向东走5公里和向南走5公里
C.收入300元和支出300元
D.使用汽油10公斤和浪费酒精10公斤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图 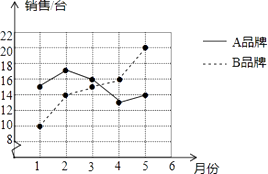
(1)分别求该商场这段时间内A,B两种品牌冰箱月销售量的中位数和方差;
(2)根据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,AC是⊙O的直径,D是![]() 的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E.
的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E. 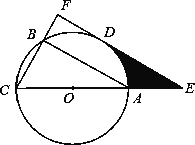
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若CF=6,∠ACB=60°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】空气的密度为0.00129g/cm3 , 0.00129这个数用科学记数法可表示为( )
A.0.129×10﹣2
B.1.29×10﹣2
C.1.29×10﹣3
D.12.9×10﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com