
【题目】已知b2-4ac是一元二次方程ax2+bx+c=0(a≠0)的一个实数根,则ab的取值范围为( )
A.ab≥ ![]()
B.ab ![]()
![]()
C.ab≥ ![]()
D.ab ![]()
![]()
【答案】B
【解析】解答:因为方程有实数解,故b2-4ac≥0.由题意有: ![]() =b2-4ac或
=b2-4ac或 ![]() =b2-4ac , 设u=
=b2-4ac , 设u= ![]() ,
,
则有2au2-u+b=0或2au2+u+b=0,(a≠0)
因为以上关于u的两个一元二次方程有实数解,
所以两个方程的判别式都大于或等于0,即得到1-8ab≥0,
所以ab≤ ![]() .
.
故选B.
分析:设u= ![]() ,利用求根公式得到关于u的两个一元二次方程,并且这两个方程都有实根,所以由判别式大于或等于0即可得到ab≤
,利用求根公式得到关于u的两个一元二次方程,并且这两个方程都有实根,所以由判别式大于或等于0即可得到ab≤ ![]()
【考点精析】关于本题考查的公式法,需要了解要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之才能得出正确答案.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】已知甲、乙两种原料中均含有A元素,其含量及每吨原料的购买单价如下表所示:
A元素含量 | 单价(万元/吨) | |
甲原料 | 5% | 2.5 |
乙原料 | 8% | 6 |
已知用甲原料提取每千克A元素要排放废气1吨,用乙原料提取每千克A元素要排放废气0.5吨,若某厂要提取A元素20千克,并要求废气排放不超过16吨,问:该厂购买这两种原料的费用最少是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE , AD与BE相交于点F . 
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
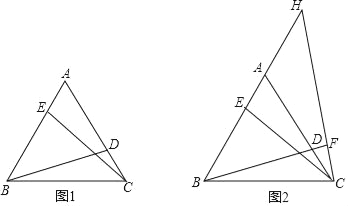
【题目】(1)如图1,点D、E分别是等边△ABC边AC、AB上的点,连接BD、CE,若AE=CD,求证:BD=CE.
(2)如图2,在(1)问的条件下,点H在BA的延长线上,连接CH交BD延长线于点F.若BF=BC,
①求证:EH=EC;
②请你找出线段AH、AD、DF之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx-5的图象经过点A(2,-1).
(1)求k的值;
(2)画出这个函数的图象;
(3)若将此函数的图象向上平移m个单位后与坐标轴围成的三角形的面积为1,请直接写出m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数y1= ![]() 的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(﹣3,m).
的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(﹣3,m).
(1)求反比例函数y1= ![]() 和一次函数y2=ax+b的表达式;
和一次函数y2=ax+b的表达式;
(2)点C 是坐标平面内一点,BC∥x 轴,AD⊥BC 交直线BC 于点D,连接AC.若AC= ![]() CD,求点C的坐标.
CD,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=mx2+(3m+1)x+3.
(1)当m取何值时,此二次函数的图象与x轴有两个交点;
(2)当抛物线y=mx2+(3m+1)x+3与x轴两个交点的横坐标均为整数,且m为正整数时,求此抛物线的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com