
【题目】已知二次函数y=mx2+(3m+1)x+3.
(1)当m取何值时,此二次函数的图象与x轴有两个交点;
(2)当抛物线y=mx2+(3m+1)x+3与x轴两个交点的横坐标均为整数,且m为正整数时,求此抛物线的表达式.
【答案】
(1)解:由题意可知,△=b2﹣4ac=(3m+1)2﹣4m×3=(3m﹣1)2>0,
解得:m≠ ![]() ,
,
∵二次函数的图象与x轴有两个交点,
∴m≠0,
∴当m≠ ![]() 且m≠0时,此二次函数的图象与x轴有两个交点
且m≠0时,此二次函数的图象与x轴有两个交点
(2)解:有求根公式,得:x= ![]() =
= ![]() ,
,
∴x1=﹣3,x2=﹣ ![]() ,
,
∵抛物线与x轴两个交点的横坐标均为整数,且m为正整数,
∴m=1,
∴抛物线的解析式为:y=x2+4x+3
【解析】(1)根据一元二次方程的根的判别式,直接计算即可;(2)根据求根公式,求出两根,由抛物线与x轴的两个交点的横坐标都为正整数,求出m的值,可得抛物线解析式.
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】已知b2-4ac是一元二次方程ax2+bx+c=0(a≠0)的一个实数根,则ab的取值范围为( )
A.ab≥ ![]()
B.ab ![]()
![]()
C.ab≥ ![]()
D.ab ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地贯彻落实国家关于“强化体育课和课外锻炼,促进青少年身心健康、体魄强健”的精神,某校大力开展体育活动.该校九年级三班同学组建了足球、篮球、乒乓球、跳绳四个体育活动小组.经调查,全班同学全员参与,各活动小组人数分布情况的扇形图和条形图如下: 
(1)求该班学生人数;
(2)请你补全条形图;
(3)求跳绳人数所占扇形圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是AC上一点,联结BD,∠CBD=∠A. 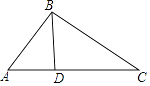
(1)求证:△CBD∽△CAB;
(2)若D是AC中点,CD=3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=x2+mx+n﹣1的对称轴为x=2. 
(1)m的值为;
(2)若抛物线与y轴正半轴交于点A,其对称轴与x轴交于点B,当△OAB是等腰直角三角形时,求n的值;
(3)点C的坐标为(3,0),若该抛物线与线段OC有且只有一个交点,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小慧根据学习函数的经验,对函数y=|x﹣1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完整: 
(1)函数y=|x﹣1|的自变量x的取值范围是;
(2)列表,找出y与x的几组对应值.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | b | 1 | 0 | 1 | 2 | … |
其中,b=;
(3)在平面直角坐标系xOy中,描出以上表中对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com