
【题目】已知甲、乙两种原料中均含有A元素,其含量及每吨原料的购买单价如下表所示:
A元素含量 | 单价(万元/吨) | |
甲原料 | 5% | 2.5 |
乙原料 | 8% | 6 |
已知用甲原料提取每千克A元素要排放废气1吨,用乙原料提取每千克A元素要排放废气0.5吨,若某厂要提取A元素20千克,并要求废气排放不超过16吨,问:该厂购买这两种原料的费用最少是多少万元?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a>0)经过原点O和点A(2,0). 
(1)写出抛物线的对称轴与x轴的交点坐标;
(2)点(x1 , y1),(x2 , y2)在抛物线上,若x1<x2<1,比较y1 , y2的大小;
(3)点B(﹣1,2)在该抛物线上,点C与点B关于抛物线的对称轴对称,求直线AC的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于点E,BF平分∠ABC,交CD于点F. 
(1)求证:DE=BF;
(2)连接EF,写出图中所有的全等三角形.(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=ax2+bx﹣3(a,b是常数)的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.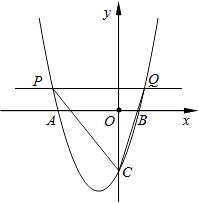
(1)求a和b的值;
(2)求t的取值范围;
(3)若∠PCQ=90°,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6cm , 点P从点A出发,沿AB方向以每秒 ![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( ).
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( ).
A.![]()
B.2
C.2 ![]()
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知b2-4ac是一元二次方程ax2+bx+c=0(a≠0)的一个实数根,则ab的取值范围为( )
A.ab≥ ![]()
B.ab ![]()
![]()
C.ab≥ ![]()
D.ab ![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com