
| A. | 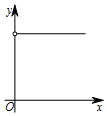 | B. | 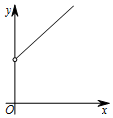 | C. | 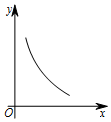 | D. |  |
分析 由于点O是△ABC的内心,根据内心的性质得到OB、OC分别平分∠ABC、∠ACB,又EF∥BC,可得到∠1=∠3,则EO=EB,同理可得FO=FC,再根据周长的所以可得到y=x+a,(x>0),即它是一次函数,即可得到正确选项.
解答 解:如图,∵点O是△ABC的内心,
∴∠1=∠2,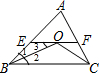
又∵EF∥BC,
∴∠3=∠2,
∴∠1=∠3,
∴EO=EB,
同理可得FO=FC,
∵x=AE+EO+FO+AF,
y=AE+BE+AF+FC+BC,
∴y=x+a,(x>0),
即y是x的一次函数,
所以B选项正确.
故选B.
点评 本题考查了一次函数y=kx+b(k≠0,k,b为常数)的图象和性质以及内心的性质和平行线的性质,正确得出函数关系式是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 45° | B. | 15° | C. | 30°或60° | D. | 45°或15° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠B=90°,∠A=60°,AB=1,作等腰三角形△ACD,使∠CAD=30°,且点D和B位于AC异侧,连结BD交AC于点O
如图,在△ABC中,∠B=90°,∠A=60°,AB=1,作等腰三角形△ACD,使∠CAD=30°,且点D和B位于AC异侧,连结BD交AC于点O查看答案和解析>>
科目:初中数学 来源: 题型:填空题
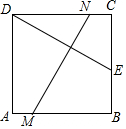 如图,将边长为8厘米的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A落在点F处,折痕为MN,则线段MN的长是4$\sqrt{5}$cm.
如图,将边长为8厘米的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A落在点F处,折痕为MN,则线段MN的长是4$\sqrt{5}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,抛物线y=-x2+20的图象与y轴正半轴的交点为A,将线段OA分成20等份,设分点分别为P1,P2,…,P19,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…,记△OP1Q1,△P1P2Q2,…的面积分别为S1,S2,…,S19,则S12+S22+…+S192的值为( )
如图,抛物线y=-x2+20的图象与y轴正半轴的交点为A,将线段OA分成20等份,设分点分别为P1,P2,…,P19,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…,记△OP1Q1,△P1P2Q2,…的面积分别为S1,S2,…,S19,则S12+S22+…+S192的值为( )| A. | 47 | B. | 47.5 | C. | 48 | D. | 48.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com