
ЁОЬтФПЁПгаетбљвЛИіЮЪЬтЃКЬНОПЭЌвЛЦНУцжБНЧзјБъЯЕжаЯЕЪ§ЛЅЮЊЕЙЪ§ЕФе§ЁЂЗДБШР§КЏЪ§y= ![]() xгыy=
xгыy= ![]() ЃЈkЁй0ЃЉЕФЭМЯѓаджЪЃЎ
ЃЈkЁй0ЃЉЕФЭМЯѓаджЪЃЎ
аЁУїИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§y= ![]() xгыy=
xгыy= ![]() ЃЌЕБkЃО0ЪБЕФЭМЯѓаджЪНјааСЫЬНОПЃЎ
ЃЌЕБkЃО0ЪБЕФЭМЯѓаджЪНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁУїЕФЬНОПЙ§ГЬЃК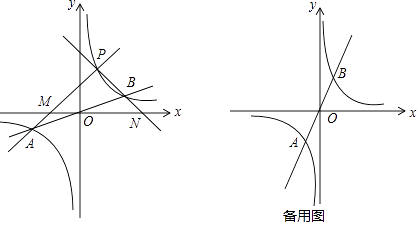
ЃЈ1ЃЉШчЭМЫљЪОЃЌЩшКЏЪ§y= ![]() xгыy=
xгыy= ![]() ЭМЯѓЕФНЛЕуЮЊAЃЌBЃЌвбжЊAЕуЕФзјБъЮЊЃЈЉkЃЌЉ1ЃЉЃЌдђBЕуЕФзјБъЮЊЃЛ
ЭМЯѓЕФНЛЕуЮЊAЃЌBЃЌвбжЊAЕуЕФзјБъЮЊЃЈЉkЃЌЉ1ЃЉЃЌдђBЕуЕФзјБъЮЊЃЛ
ЃЈ2ЃЉШєЕуPЮЊЕквЛЯѓЯоФкЫЋЧњЯпЩЯВЛЭЌгкЕуBЕФШЮвтвЛЕуЃЎ
ЂйЩшжБЯпPAНЛxжсгкЕуMЃЌжБЯпPBНЛxжсгкЕуNЃЎЧѓжЄЃКPM=PNЃЎ
жЄУїЙ§ГЬШчЯТЃЌЩшPЃЈmЃЌ ![]() ЃЉЃЌжБЯпPAЕФНтЮіЪНЮЊy=ax+bЃЈaЁй0ЃЉЃЎ
ЃЉЃЌжБЯпPAЕФНтЮіЪНЮЊy=ax+bЃЈaЁй0ЃЉЃЎ
дђ  ЃЌ
ЃЌ
НтЕУ ![]()
ЁржБЯпPAЕФНтЮіЪНЮЊ ![]()
ЧыФуАбЩЯУцЕФНтД№Й§ГЬВЙГфЭъећЃЌВЂЭъГЩЪЃгрЕФжЄУїЃЎ
ЂкЕБPЕузјБъЮЊЃЈ1ЃЌkЃЉЃЈkЁй1ЃЉЪБЃЌХаЖЯЁїPABЕФаЮзДЃЌВЂгУkБэЪОГіЁїPABЕФУцЛ§ЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉЃЈkЃЌ1ЃЉ
ЃЈ2ЃЉ
ЂкНтЃКгЩЂйПЩжЊЃЌдкЁїPMNжаЃЌPM=PNЃЌ
ЁрЁїPMNЮЊЕШбќШ§НЧаЮЃЌЧвMH=HN=kЃЎ
ЕБPЕузјБъЮЊЃЈ1ЃЌkЃЉЪБЃЌPH=kЃЌ
ЁрMH=HN=PHЃЌ
ЁрЁЯPMH=ЁЯMPH=45ЁуЃЌЁЯPNH=ЁЯNPH=45ЁуЃЌ
ЁрЁЯMPN=90ЁуЃЌМДЁЯAPB=90ЁуЃЌ
ЁрЁїPABЮЊжБНЧШ§НЧаЮЃЎ
ЕБkЃО1ЪБЃЌШчЭМ1ЃЌ
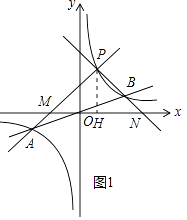
SЁїPAB=SЁїPMNЉSЁїOBN+SЁїOAMЃЌ
= ![]() MNPHЉ
MNPHЉ ![]() ONyB+
ONyB+ ![]() OM|yA|ЃЌ
OM|yA|ЃЌ
= ![]() ЁС2kЁСkЉ
ЁС2kЁСkЉ ![]() ЃЈk+1ЃЉЁС1+
ЃЈk+1ЃЉЁС1+ ![]() ЃЈkЉ1ЃЉЁС1ЃЌ
ЃЈkЉ1ЃЉЁС1ЃЌ
=k2Љ1ЃЛ
ЕБ0ЃМkЃМ1ЪБЃЌШчЭМ2ЃЌ

SЁїPAB=SЁїOBNЉSЁїPMN+SЁїOAMЃЌ
= ![]() ONyBЉk2+
ONyBЉk2+ ![]() OM|yA|ЃЌ
OM|yA|ЃЌ
= ![]() ЃЈk+1ЃЉЁС1Љk2+
ЃЈk+1ЃЉЁС1Љk2+ ![]() ЃЈ1ЉkЃЉЁС1ЃЌ
ЃЈ1ЉkЃЉЁС1ЃЌ
=1Љk2
ЁОНтЮіЁПНтЃКЃЈ1ЃЉгЩе§ЁЂЗДБШР§КЏЪ§ЭМЯѓЕФЖдГЦадПЩжЊЃЌЕуAЁЂBЙигкдЕуOЖдГЦЃЌ
ЁпAЕуЕФзјБъЮЊЃЈЉkЃЌЉ1ЃЉЃЌ
ЁрBЕуЕФзјБъЮЊЃЈkЃЌ1ЃЉЃЎ
ЫљвдД№АИЪЧЃКЃЈkЃЌ1ЃЉЃЎ
2ЃЉЂйжЄУїЙ§ГЬШчЯТЃЌЩшPЃЈmЃЌ ![]() ЃЉЃЌжБЯпPAЕФНтЮіЪНЮЊy=ax+bЃЈaЁй0ЃЉЃЎ
ЃЉЃЌжБЯпPAЕФНтЮіЪНЮЊy=ax+bЃЈaЁй0ЃЉЃЎ
дђ  ЃЌ
ЃЌ
НтЕУЃК 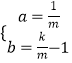 ЃЌ
ЃЌ
ЁржБЯпPAЕФНтЮіЪНЮЊy= ![]() x+
x+ ![]() Љ1ЃЎ
Љ1ЃЎ
ЕБy=0ЪБЃЌx=mЉkЃЌ
ЁрMЕуЕФзјБъЮЊЃЈmЉkЃЌ0ЃЉЃЎ
Й§ЕуPзїPHЁЭxжсгкHЃЌШчЭМ1ЫљЪОЃЌ
ЁпPЕузјБъЮЊЃЈmЃЌ ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрHЕуЕФзјБъЮЊЃЈmЃЌ0ЃЉЃЌ
ЁрMH=xHЉxM=mЉЃЈmЉkЃЉ=kЃЎ
ЭЌРэПЩЕУЃКHN=kЃЎ
ЁрMH=HNЃЌ
ЁрPM=PNЃЎ
ЫљвдД№АИЪЧЃК  ЃЛy=
ЃЛy= ![]() x+
x+ ![]() Љ1ЃЎ
Љ1ЃЎ
ЁОПМЕуОЋЮіЁПНтД№ДЫЬтЕФЙиМќдкгкРэНтЗДБШР§КЏЪ§ЕФЭМЯѓЕФЯрЙижЊЪЖЃЌеЦЮеЗДБШР§КЏЪ§ЕФЭМЯёЪєгкЫЋЧњЯпЃЎЗДБШР§КЏЪ§ЕФЭМЯѓМШЪЧжсЖдГЦЭМаЮгжЪЧжааФЖдГЦЭМаЮЃЎгаСНЬѕЖдГЦжсЃКжБЯпy=xКЭ y=-xЃЎЖдГЦжааФЪЧЃКдЕуЃЌвдМАЖдЗДБШР§КЏЪ§ЕФаджЪЕФРэНтЃЌСЫНтаджЪ:ЕБkЃО0ЪБЫЋЧњЯпЕФСНжЇЗжБ№ЮЛгкЕквЛЁЂЕкШ§ЯѓЯоЃЌдкУПИіЯѓЯоФкyжЕЫцxжЕЕФдіДѓЖјМѕаЁЃЛ ЕБkЃМ0ЪБЫЋЧњЯпЕФСНжЇЗжБ№ЮЛгкЕкЖўЁЂЕкЫФЯѓЯоЃЌдкУПИіЯѓЯоФкyжЕЫцxжЕЕФдіДѓЖјдіДѓЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃКдке§ЗНаЮЭјИёжагавЛИіЁїABCЃЌАДвЊЧѓНјааЯТСазїЭМ(жЛФмНшжњгкЭјИё)ЃЎ
(1)ЛГіЁїABCжаBCБпЩЯЕФИпAHКЭBCБпЩЯЕФжаЯпADЃЎ
(2)ЛГіНЋЁїABCЯђгвЦНвЦ5ИёгжЯђЩЯЦНвЦ3ИёКѓЕФЁїAЁфBЁфCЁфЃЎ
(3)ЁїABCЕФУцЛ§ЮЊЁЁ ЁЁЃЎ
(4)ШєСЌНгAAЁфЃЌCCЁфЃЌдђетСНЬѕЯпЖЮжЎМфЕФЙиЯЕЪЧЁЁ ЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЃЌЙ§ЕуCЕФжБЯпMNЁЮABЃЌDЮЊABБпЩЯвЛЕуЃЌЙ§ЕуDзїDEЁЭBCЃЌНЛжБЯпMNгкEЃЌДЙзуЮЊFЃЌСЌНгCDЃЌBE
ЃЈ1ЃЉЧѓжЄЃКCE=AD
ЃЈ2ЃЉЕБЕуDдкABжаЕуЪБЃЌЫФБпаЮBECDЪЧЪВУДЬиЪтЫФБпаЮЃПЫЕУїРэгЩ
ЃЈ3ЃЉШєDЮЊABЕФжаЕуЃЌдђЕБЁЯAЕФДѓаЁТњзуЪВУДЬѕМўЪБЃЌЫФБпаЮBECDЪЧе§ЗНаЮЃПЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈдФЖСВФСЯЃЉ
аЁУїЭЌбЇгіЕНЯТСаЮЪЬтЃК
НтЗНГЬзщ ЃЌЫћЗЂЯжШчЙћжБНггУДњШыЯћдЊЗЈЛђМгМѕЯћдЊЗЈЧѓНтЃЌдЫЫуСПБШНЯДѓЃЌвВШнвзГіДэЃЎШчЙћАбЗНГЬзщжаЕФЃЈ2x+3yЃЉПДзївЛИіЪ§ЃЌАбЃЈ2xЉ3yЃЉПДзївЛИіЪ§ЃЌЭЈЙ§ЛЛдЊЃЌПЩвдНтОіЮЪЬтЃЎвдЯТЪЧЫћЕФНтЬтЙ§ГЬЃК
ЃЌЫћЗЂЯжШчЙћжБНггУДњШыЯћдЊЗЈЛђМгМѕЯћдЊЗЈЧѓНтЃЌдЫЫуСПБШНЯДѓЃЌвВШнвзГіДэЃЎШчЙћАбЗНГЬзщжаЕФЃЈ2x+3yЃЉПДзївЛИіЪ§ЃЌАбЃЈ2xЉ3yЃЉПДзївЛИіЪ§ЃЌЭЈЙ§ЛЛдЊЃЌПЩвдНтОіЮЪЬтЃЎвдЯТЪЧЫћЕФНтЬтЙ§ГЬЃК
СюmЃН2x+3yЃЌnЃН2xЉ3yЃЌ
етЪБдЗНГЬзщЛЏЮЊ ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
Аб![]() ДњШыmЃН2x+3yЃЌnЃН2xЉ3yЃЎ
ДњШыmЃН2x+3yЃЌnЃН2xЉ3yЃЎ
ЕУ![]() НтЕУ
НтЕУ![]() ЃЎ
ЃЎ
ЫљвдЃЌдЗНГЬзщЕФНтЮЊ![]()
ЃЈНтОіЮЪЬтЃЉ
ЧыФуВЮПМаЁУїЭЌбЇЕФзіЗЈЃЌНтОіЯТУцЕФЮЪЬтЃК
ЃЈ1ЃЉНтЗНГЬзщ ЃЛ
ЃЛ
ЃЈ2ЃЉвбжЊЗНГЬзщ![]() ЕФНтЪЧ
ЕФНтЪЧ![]() ЃЌЧѓЗНГЬзщ
ЃЌЧѓЗНГЬзщ![]() ЕФНтЃЎ
ЕФНтЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊЪЪгІШевцМЄСвЕФЪаГЁОКељвЊЧѓЃЌФГЙЄГЇДг2016Фъ1дТЧвПЊЪМЯоВњЃЌВЂЖдЩњВњЯпНјааЮЊЦк5ИідТЕФЩ§НЕИФдьЃЌИФдьЦкМфЕФдТРћШѓгыЪБМфГЩЗДБШР§ЃЛЕН5дТЕзПЊЪМЛжИДШЋУцЩњВњКѓЃЌЙЄГЇУПдТЕФРћШѓЖМБШЧАвЛИідТдіМг10ЭђдЊЃЎЩш2016Фъ1дТЮЊЕк1ИідТЃЌЕкxИідТЕФРћШѓЮЊyЭђдЊЃЌЦфЭМЯѓШчЭМЫљЪОЃЌЪдНтОіЯТСаЮЪЬтЃК 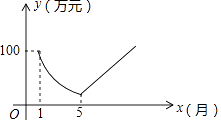
ЃЈ1ЃЉЗжБ№ЧѓИУЙЄГЇЖдЩњВњЯпНјааЩ§МЖИФдьЧАКѓЃЌyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЕНЕкМИИідТЪБЃЌИУЙЄГЇдТРћШѓВХФмдйДЮДяЕН100ЭђдЊЃП
ЃЈ3ЃЉЕБдТРћШѓЩйгк50ЭђдЊЪБЃЌЮЊИУЙЄГЇЕФзЪН№НєеХЦкЃЌЮЪИУЙЄГЇзЪН№НєеХЦкЙВгаМИИідТЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМХзЮяЯпy=ax2+bx+cЕФЭМЯѓНЛxжсгкAЃЈЉ2ЃЌ0ЃЉКЭЕуBЃЌНЛyжсИКАыжсгкЕуCЃЌЧвOB=OCЃЌЯТСаНсТлЃК
Ђй2bЉc=2ЃЛЂкa= ![]() ЃЛЂлac=bЉ1ЃЛЂм
ЃЛЂлac=bЉ1ЃЛЂм ![]() ЃО0
ЃО0
Цфжае§ШЗЕФИіЪ§гаЃЈ ЃЉ
A.1Иі
B.2Иі
C.3Иі
D.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЁїABCжаЃЌBDЁЭACгкЕуDЃЎ
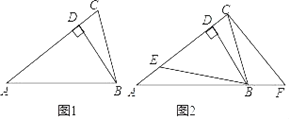
ЃЈ1ЃЉШєЁЯCЃНЁЯABCЃН2ЁЯAЃЌдђЁЯDBCЃНЁЁ ЁЁЁуЃЛ
ЃЈ2ЃЉШєЁЯAЃН2ЁЯCBDЃЌЧѓжЄЃКЁЯACBЃНЁЯABCЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌEЪЧADЩЯвЛЕуЃЌFЪЧABбгГЄЯпЩЯвЛЕуЃЌСЌНгBEЁЂCFЃЌЪЙЁЯBECЃНЁЯCFBЃЌЁЯBCFЃН2ЁЯABEЃЌЧѓЁЯEBCЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬШЫНЋЕЅМлЮЊ8дЊЕФЩЬЦЗАДУПМў10дЊГіЪлЃЌУПЬьПЩЯњЪл100МўЃЌвбжЊетжжЩЬЦЗУПЬсИп2дЊЃЌЦфЯњСПОЭвЊМѕЩй10МўЃЌЮЊСЫЪЙУПЬьЫљзЌРћШѓзюЖрЃЌИУЩЬШЫгІНЋЯњЪлМлЃЈЮЊХМЪ§ЃЉЬсИпЃЈ ЃЉ
A.8дЊЛђ10дЊ
B.12дЊ
C.8дЊ
D.10дЊ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAЃЈ2ЃЌ0ЃЉЃЌDЃЈ6ЃЌ4ЃЉЃЌНЋЯпЖЮADЦНвЦЕУЕНBCЃЌBЃЈ0ЃЌЉ6ЃЉЃЌбгГЄBCНЛxжсгкЕуEЃЎ
ЃЈ1ЃЉдђЁїABCЕФУцЛ§ЪЧЁЁ ЃЛ
ЃЈ2ЃЉQЮЊxжсЩЯвЛЖЏЕуЃЌЕБЁїABCгыЁїADQЕФУцЛ§ЯрЕШЪБЃЌЪдЧѓЕуQЕФзјБъЃЎ
ЃЈ3ЃЉШєДцдквЛЕуMЃЈmЃЌ6ЃЉЧвЁїADMЕФУцЛ§ВЛаЁгкЁїABCЕФУцЛ§ЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com