
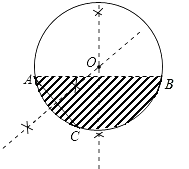
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面. 
(1)请你补全这个输水管道的圆形截面;
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
【答案】
(1)解:先作弦AB的垂直平分线;在弧AB上任取一点C连接AC,作弦AC的垂直平分线,两线交点作为圆心O,OA作为半径,画圆即为所求图形.
(2)解:过O作OE⊥AB于D,交弧AB于E,连接OB.
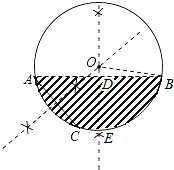
∵OE⊥AB
∴BD= ![]() AB=
AB= ![]() ×16=8cm
×16=8cm
由题意可知,ED=4cm
设半径为xcm,则OD=(x﹣4)cm
在Rt△BOD中,由勾股定理得:
OD2+BD2=OB2
∴(x﹣4)2+82=x2
解得x=10.
即这个圆形截面的半径为10cm
【解析】如图所示,根据垂径定理得到BD= ![]() AB=
AB= ![]() ×16=8cm,然后根据勾股定理列出关于圆形截面半径的方程求解.
×16=8cm,然后根据勾股定理列出关于圆形截面半径的方程求解.
【考点精析】根据题目的已知条件,利用勾股定理的概念和垂径定理的推论的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;推论1:A、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧B、弦的垂直平分线经过圆心,并且平分弦所对的两条弧C、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;推论2 :圆的两条平行弦所夹的弧相等.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
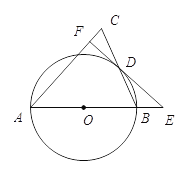
【题目】如图,在△ABC中,以AB为直径的⊙O交BC于点D,CD=BD,过点D作⊙O的切线交边AC于点F,交AB的延长线于点E.
(1)求证:EF⊥AC;
(2)若AF=9,EF=12,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
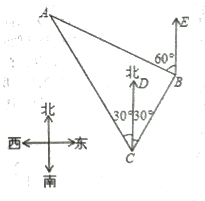
【题目】如图,我国渔政船在钓鱼岛海域C处测得钓鱼岛A在渔政船的北偏西30。的方向上,随后渔政船以80海里/小时的速度向北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在渔政船的北偏西60°的方向上,求此时渔政船距钓鱼岛A的距离姓B.(结果保留小数点后一位,其中![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店销售一批衬衣,每件进价250元,开始以每件400元的价格销售,每星期能卖出20件,后来因库存积压,决定降价销售,经过两次降价后每件售价为324元,求每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
通过整式运算一章的学习,我们发现要验证一个结论的正确性可以有两种方法:
例如:要验证结论![]()
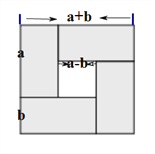
方法1:几何图形验证:如下图,我们可以将一个边长为(a+b)的正方形上裁去一个边长为(a-b)的小正方形则剩余图形的面积为4ab,验证该结论正确。
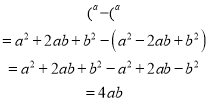
方法2:代数法验证:等式左边=![]() ,
,
所以,左边=右边,结论成立。
观察下列各式:
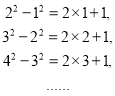
(1)按规律,请写出第n个等式________________;
(2)试分别用两种方法验证这个结论的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知直线AC的函数解析式为y= ![]() x+8,点P从点A开始沿AO方向以1个单位/秒的速度运动,点Q从O点开始沿OC方向以2个单位/秒的速度运动.如果P、Q两点分别从点A、点O同时出发,经过多少秒后能使△POQ的面积为8个平方单位?
x+8,点P从点A开始沿AO方向以1个单位/秒的速度运动,点Q从O点开始沿OC方向以2个单位/秒的速度运动.如果P、Q两点分别从点A、点O同时出发,经过多少秒后能使△POQ的面积为8个平方单位? 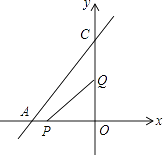
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com