
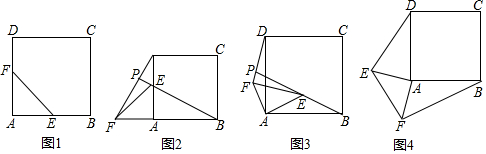
���� ��1����֤��AEB�ա�AFD�ã���DPE=��DAB=90�㣬���ݹ��ɶ�����BE=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$������ͬ�ǵ����Ǻ�����ʽ����BP�ij���
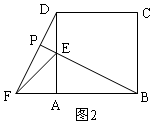
��2��BE=DF��BE��DF��ͬ����֤����AEB�ա�AFD������BE=DF����FDA=��ABE������������������������Ƕ�Ӧ��ȣ����������Ҳ��Ӧ��ȵã���DPM=��MAB=90�㣬��BP��DF��
��3����ͼ4����Ϊ��ͼ���п�����AED���AFB������Ӧ�߷ֱ�Ϊ�����εı߳�AB��AD��ֻҪ֤����Ӧ���ϵĸ���ȼ��ɣ�����EG��FH��֤����AEG�ա�AFH�ɵý��ۣ�
���  �⣺��1�����ı���ABCDΪ�����Σ�
�⣺��1�����ı���ABCDΪ�����Σ�
��AB=AD=4����DAB=90�㣬
��ͼ1����E��F�ֱ���������ABCD�ı�AB��AD���е㣬
��AE=AF=2��
����ת�ã�ͼ2�е�AE=AF=2��
�ڡ�AFD�͡�AEB�У�
��$\left\{\begin{array}{l}{AE=AF}\\{��EAB=��FAD=90��}\\{AB=AD}\end{array}\right.$��
���AFD�ա�AEB��SAS����
���ADF=��ABE��
�ߡ�AEB=��DEP��
���DPE=��DAB=90�㣬
��Rt��AEB��AE=2��AB=4��
�ɹ��ɶ����ã�BE=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$��
cos��ABE=$\frac{BP}{BF}=\frac{AB}{BE}$��
��$\frac{BP}{2+4}=\frac{4}{2\sqrt{5}}$��
BP=$\frac{12\sqrt{5}}{5}$��
��2��BE=DF��BE��DF��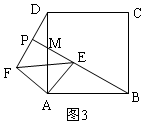
�������£�
����ת�ã���EAB=��FAD��
��AE=AF��AB=AD��
���AEB�ա�AFD��
��BE=DF����FDA=��ABE��
�ߡ�PMD=��AMB��
���DPM=��MAB=90�㣬
��BP��DF����BE��DF��
��3����ͼ4����AED���AFB�������ȣ������ǣ�
��F��FH��AB����BA�ӳ�����H����E��EG��AD��G��
�ߡ�EAF=90�㣬
���EAH+��FAH=90�㣬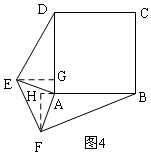
�ߡ�HAD=90�㣬
���EAH+��EAG=90�㣬
���FAH=��EAG��
��AE=AF����EGA=��AHF=90�㣬
���AEG�ա�AFH��
��EG=FH��
��S��AED=$\frac{1}{2}$AD•EG��
S��ABF=$\frac{1}{2}$AB•FH��
��AB=AD��
��S��AED=S��AFB��
���� �������ı����ۺ��⣬��Ҫ������ȫ�������ε��ж������ʣ����ɶ�����ֱ�������ε����ʺ���ת�����ʣ��dz������ͣ������ʵĹؼ������������ߣ����������ߣ�


 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����O�İ뾶Ϊ2cm����BC����AD���ڵ�E���ҡ�CED=75�㣬��ABΪ$2\sqrt{2}$cm����CD�ij�Ϊ2cm��
��ͼ����O�İ뾶Ϊ2cm����BC����AD���ڵ�E���ҡ�CED=75�㣬��ABΪ$2\sqrt{2}$cm����CD�ij�Ϊ2cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y1��y2��y3 | B�� | y1��y3��y2 | C�� | y3��y1��y2 | D�� | y2��y1��y3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
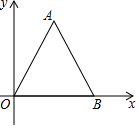 ��ƽ��ֱ������ϵ�У��ȱߡ�AOB��λ����ͼ����OB=3�����A������Ϊ��$\frac{3}{2}$��$\frac{3\sqrt{3}}{2}$����
��ƽ��ֱ������ϵ�У��ȱߡ�AOB��λ����ͼ����OB=3�����A������Ϊ��$\frac{3}{2}$��$\frac{3\sqrt{3}}{2}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
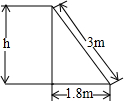 ��ͼ��һ�ܳ�3m������б����ǽ�ϣ����ӵĵ˵�ǽ�ǵľ���Ϊ1.8m�������Ӷ��˵�����ľ���hΪ2.4m��
��ͼ��һ�ܳ�3m������б����ǽ�ϣ����ӵĵ˵�ǽ�ǵľ���Ϊ1.8m�������Ӷ��˵�����ľ���hΪ2.4m���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
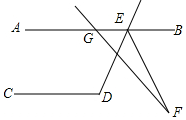 ��ͼ��AB��CD����CDE=116�㣬GF����DEB��ƽ����EF�ڵ�F����AGF=130�㣬���F=8�㣮
��ͼ��AB��CD����CDE=116�㣬GF����DEB��ƽ����EF�ڵ�F����AGF=130�㣬���F=8�㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com