
【题目】如图O是边长为9的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于点F,OE∥AC,交BC于点E,则OD+OE+OF的值为( )
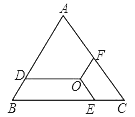
A. 3 B. 6 C. 8 D. 9
科目:初中数学 来源: 题型:
【题目】如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?( ) 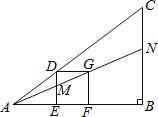
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是边BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③四边形AEPF的面积=△ABC的面积的一半,④当EF最短时,EF=AP,上述结论始终正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABO中,AB⊥OB,OB= ![]() ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为( )
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为( ) 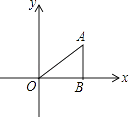
A.(﹣1,﹣ ![]() )
)
B.(﹣1,﹣ ![]() )或(﹣2,0)
)或(﹣2,0)
C.(﹣ ![]() ,1)或(0,﹣2)
,1)或(0,﹣2)
D.(﹣ ![]() ,1)
,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积进行了证明.著名数学家华罗庚提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
请根据图1中直角三角形叙述勾股定理.

以图1中的直角三角形为基础,可以构造出以a,b为底,以a+b为高的直角梯形(如图2).请你利用图2,验证勾股定理;
利用图2中的直角梯形,我们可以证明![]() .其证明步骤如下:
.其证明步骤如下:
∵BC=a+b,AD=_____;
又∵在直角梯形ABCD中有BC_____AD(填大小关系),即_____.
∴![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF= ![]() AB.
AB.
(3)如图3,若∠EDF的两边分别交AB,AC的延长线于E、F两点,(2)中的结论还成立吗?如果成立,请证明;如果不成立,请直接写出线段BE,AB,CF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到离A的距离等于___________时,ΔABC和ΔPQA全等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com