
【题目】如图1,已知在长方形ABCD中, AD=8, AB=4,将长方形ABCD沿着对角线BD折叠,使点C落在 ![]() 处,
处, ![]() 交AD于点E.
交AD于点E.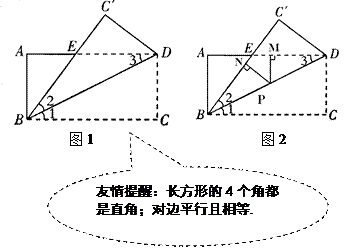
(1)求证:△BED是等腰三角形.
(2)求DE的长.
(3)如图2,若点P是BD上一动点, ![]() 于点N,
于点N, ![]() 于点M,问: PN+PM的长是否为定值?如果是,请求出该值,如果不是,请说明理由.
于点M,问: PN+PM的长是否为定值?如果是,请求出该值,如果不是,请说明理由.
【答案】
(1)解:由翻折知,∠1=∠2 ,
∵AD∥BC,
∴∠3=∠2 ,
∴∠1=∠3,
∴BE=DE,
即△BED是等腰三角形
(2)解:设DE=x,则AE=8-x,BE=x,
在Rt△ABE中, ![]()
解之, x=5, ∴ DE=5
(3)解:PM+PN为定值,是4 ,
延长MP,交BC于点H,
∵AD∥BC,PM ![]() ,
,
∴PH⊥BC,
∵∠1=∠2, PN ![]() ,PH⊥BC,
,PH⊥BC,
∴PN=PH ,
∴ PM+PN=MN=AB=4
【解析】(1)根据折叠的性质,得到∠1=∠2 ,由AD∥BC,得到内错角相等得到∠3=∠2 ,即∠1=∠3,根据等角对等边得到BE=DE, 即△BED是等腰三角形;(2)在Rt△ABE中,根据勾股定理求出DE的长;(3)根据题意作出辅助线,得到PH⊥BC,再由∠1=∠2,得到PN=PH ,得到PM+PN=MN=AB的值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=3,AD=2,分别以边AD,BC为直径在矩形ABCD的内部作半圆O1和半圆O2,一平行于AB的直线EF与这两个半圆分别交于点E、点F,且EF=2(EF与AB在圆心O1和O2的同侧),则由![]() ,EF,
,EF,![]() ,AB所围成图形(图中阴影部分)的面积等于 .
,AB所围成图形(图中阴影部分)的面积等于 .
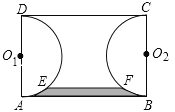
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地新建的一个企业,每月将生产1960吨污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号种选择:
污水处理器型号 | A型 | B型 |
处理污水能力(吨/月) | 240 | 180 |
已知商家售出的2台A型、3台B型污水处理器的总价为44万元,售出的1台A型、4台B型污水处理器的总价为42万元.
(1)求每台A型、B型污水处理器的价格;
(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么他们至少要支付多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,属于必然事件的是( )
A.明天我市下雨
B.抛一枚硬币,正面朝上
C.走出校门,看到的第一辆汽车的牌照的末位数字是偶数
D.一个口袋中装有2个红球和一个白球,从中摸出2个球,其中有红球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据河南省发改委发布消息,2016年全省固定资产投资继续保持持续稳定增长,全年完成39753亿元,总量居全国第3位.将数据39753亿用科学记数法表示为( )
A.3.9753×109
B.0.39753×1010
C.39.753×1011
D.3.9753×1012
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:
各版面选择人数的扇形统计图 各版面选择人数的条形统计图
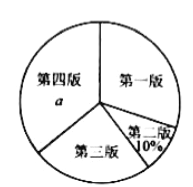

请根据图中信息,解答下列问题:
(1)该调查的样本容量为 ,![]()
![]() ,“第一版”对应扇形的圆心角为
,“第一版”对应扇形的圆心角为 ![]() ;
;
(2)请你补全条形统计图;
(3)若该校有![]() 名学生,请你估计全校学生中最喜欢“第一版”的人数.
名学生,请你估计全校学生中最喜欢“第一版”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探索发现】
如图①,是一张直角三角形纸片,∠B=60°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
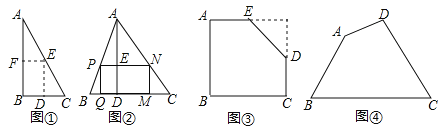
【拓展应用】
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
【灵活应用】
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
【实际应用】
如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com