
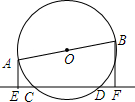
 圆O的直径AB=10cm,CD长是圆O的$\frac{1}{6}$,AE⊥CD于E,BF⊥CD于F.
圆O的直径AB=10cm,CD长是圆O的$\frac{1}{6}$,AE⊥CD于E,BF⊥CD于F.分析 (1)过点O作OG⊥CD于G,则AE∥OG∥BF,根据平行线分线段成比例定理与垂径定理即可证明;
(2)OG是直角梯形ABFE的中位线,则AE+BF=2OG,连接OC,根据勾股定理和垂径定理即可求得OG的长,进而求解.
解答 (1)证明:过点O作OG⊥CD于G,
∵AE⊥EF,OG⊥EF,BF⊥EF,
∴AE∥OG∥BF,
∴$\frac{OA}{OB}$=$\frac{GE}{GF}$,
又∵OA=OB,
∴GE=GF,
∵OG过圆心O,OG⊥CD,
∴CG=GD,
∴EG-CG=GF-GD,
即CE=DF;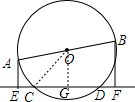
(2)解:连接OC,则OC=$\frac{1}{2}$AB=5,
∵OG过圆心O,OG⊥CD,
∴CG=$\frac{1}{2}$CD,
∵CD长是圆O的$\frac{1}{6}$,
∴CG=$\frac{1}{12}$×10π≈2.5,
∴OG=$\sqrt{{5}^{2}-(\frac{5}{2})^{2}}$=$\frac{5}{2}$$\sqrt{3}$,
∵梯形ABFE中,EG=GF,AO=OB,
∴OG=$\frac{1}{2}$(AE+BF),
∴AE+BF=2OG=5$\sqrt{3}$.
点评 本题主要考查了垂径定理的应用,利用垂径定理可以把求弦长或圆心角的问题转化为解直角三角形的问题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:初中数学 来源: 题型:解答题
 已知等边三角形ABC的边长为2,将这个三角形放置在如图所示的直角坐标系中,且B,C两点的坐标分别为(-1,0),(1,0)
已知等边三角形ABC的边长为2,将这个三角形放置在如图所示的直角坐标系中,且B,C两点的坐标分别为(-1,0),(1,0)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10n | B. | $\frac{n}{10}$ | C. | 10m | D. | $\frac{m}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com